Overflow during computation

Question

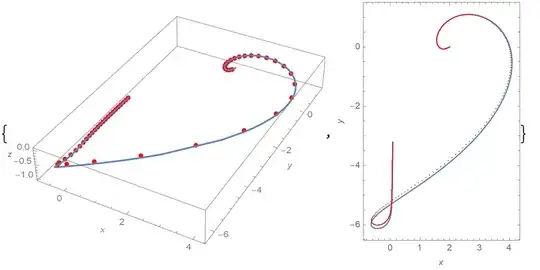
The following code display the Predictor-Corrector approach to solve the four dimensional Fractional-Order Delay Differential system,

The below code works fine for some values of $\tau$ but it gives an overflow error message for other values of $\tau$ for example, when $\tau=0.10$ and n=4500(smax=300 in the code) I get error message which says that an overflow occurred during computation.

a1 = 2.1; b1 = 0.01;
c1 = 2.6;
Subscript[m, 1] = 8.4;
Subscript[m, 2] = 6.4;
Subscript[m, 3] = 2.2;
f[t_, x_, y_, z_, w_] := x*(y - a1) + (Subscript[m, 1]* w) + z;
g[t_, x_, y_, z_, w_] := -(b1*y) + (Subscript[m, 2]* w) - x^2 + 1;
d[t_, x_, y_, z_, w_] := -(c1*z) + (Subscript[m, 3]* w) - x;
q[t_, x_, y_, z_, w_] := -x*y*z;
\[Alpha] = 0.93;
h = 0.01;
t[0] = 0;
x0 = 2;
y0 = 0;
z0 = -0.2;
w0 = 0.4;
tau = 0.10; nn = Round[tau/h]; smax = 300; n = nn*smax;
Do[x[i] = x0; y[i] = y0; z[i] = z0; w[i] = w0;, {i, -nn, 0}];
For[k = 1, k <= n, k++, b[k] = k^\[Alpha] - (k - 1)^\[Alpha]; 
  a[k] = -(2*k^(\[Alpha] + 1)) + (k - 1)^(\[Alpha] + 1) + (k + 
       1)^(\[Alpha] + 1);];
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn];, {i, 0, s*nn}]; 
 For[j = (s - 1)*nn + 1, j <= s*nn, j++, t[j] = j*h; 
  p[j] = (h^\[Alpha]*
       Sum[b[j - A]*f[A*h, x[A], y1[A], z[A], w[A]], {A, 0, j - 1}])/
     Gamma[\[Alpha] + 1] + x[0];
  l[j] = (h^\[Alpha]*
       Sum[b[j - B]*g[B*h, x1[B], y[B], z[B], w[B]], {B, 0, j - 1}])/
     Gamma[\[Alpha] + 1] + y[0]; 
  r[j] = (h^\[Alpha]*
       Sum[b[j - C]*d[C*h, x1[C], y[C], z[C], w[C]], {C, 0, j - 1}])/
     Gamma[\[Alpha] + 1] + z[0];
  o[j] = (h^\[Alpha]*
       Sum[b[j - H]*q[H*h, x[H], y[H], z[H], w[H]], {H, 0, j - 1}])/
     Gamma[\[Alpha] + 1] + w[0];
  x[j] = (h^\[Alpha]*(Sum[
          a[j - K]*f[h*K, x[K], y1[K], z[K], w[K]], {K, 1, j - 1}] + 
         f[h*j, p[j], l[j], r[j], 
          o[j]] + ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*
             j^\[Alpha])*f[0, x[0], y[0], z[0], w[0]]))/
     Gamma[\[Alpha] + 2] + x[0];
  y[j] = (h^\[Alpha]*(Sum[
          a[j - F]*g[F*h, x1[F], y[F], z[F], w[F]], {F, 1, j - 1}] + 
         g[h*j, p[j], l[j], r[j], 
          o[j]] + ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*
             j^\[Alpha])*g[0, x[0], y[0], z[0], w[0]]))/
     Gamma[\[Alpha] + 2] + y[0];
  z[j] = (h^\[Alpha]*(Sum[
          a[j - G]*d[G*h, x1[G], y[G], z[G], w[G]], {G, 1, j - 1}] + 
         d[h*j, p[j], l[j], r[j],
      o[j]] + ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*
         j^\[Alpha])*d[0, x[0], y[0], z[0], w[0]]))/
 Gamma[\[Alpha] + 2] + z[0];

w[j] = (h^[Alpha](Sum[
          a[j - R]q[Rh, x1[R], y[R], z[R], w[R]], {R, 1, j - 1}] + 
         q[hj, p[j], l[j], r[j], 
          o[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)*
             j^[Alpha])*q[0, x[0], y[0], z[0], w[0]]))/
     Gamma[[Alpha] + 2] + w[0];];, {s, 1, smax}]
lst = Table[{t[i], x[i]}, {i, n}];
lst1 = Table[{x[i], y[i], z[i]}, {i, n}];
ListLinePlot[lst, PlotRange -> Full, 
  Frame -> True, PlotLabel -> "[Alpha]=0.93,[Tau]=0.10", 
 FrameStyle -> Black, 
  FrameLabel -> {t, x}, LabelStyle -> Directive[Blue, Bold], 
  PlotStyle -> Purple]
 ListPointPlot3D[lst1, PlotRange -> Full, 
  AxesLabel -> {x, y, z}, PlotLabel -> "[Alpha]=0.93,[Tau]=0.10", 
  LabelStyle -> Directive[Black, Bold, FontFamily -> "Helvetica"], 
  TicksStyle -> Black, PlotStyle -> Purple]

Could anyone please solve this issue.

Answer 1

We can use last code from my answer here extended with taken account new variable and functions. First, we test code for $alpha=1$ to compare with NDSolve[]

a1 = 2.1; b1 = 0.01; 
c1 = 2.6; m1 = 8.4; m2 = 6.4; m3 = 2.2; 
f1[t_, x_, y_, z_, w_] := x*(y - a1) + z + m1*w; 
f2[t_, x_, y_, z_, w_] := -(b1*y) - x^2 + 1 + m2*w; 
f3[t_, x_, y_, z_, w_] := -(c1*z) - x + m3*w; 
f4[t_, x_, y_, z_, w_] := (-x)*y*z
\[Alpha] = 1; 
h = 0.01; 
x0 = 2; 
y0 = 0; 
z0 = -0.2; w0 = 0.4; tau = 0.1; tmax = 5; nn = Round[tau/h]; smax = Round[tmax/tau]; 
  n = nn*smax; Do[x[i] = x0; y[i] = y0; z[i] = z0; w[i] = w0; , {i, -nn, 0}]; 
For[k = 1, k <= n, k++, b[k] = k^\[Alpha] - (k - 1)^\[Alpha]; 
    a[k] = -(2*k^(\[Alpha] + 1)) + (k - 1)^(\[Alpha] + 1) + (k + 1)^(\[Alpha] + 1); ]; 
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn]; , {i, 0, s*nn}]; 
   For[j = (s - 1)*nn + 1, j <= s*nn, j++, 
    p1[j] = (h^\[Alpha]*Sum[b[j - A]*f1[A*h, x[A], y1[A], z[A], w[A]], {A, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + x[0]; 
     p2[j] = (h^\[Alpha]*Sum[b[j - B]*f2[B*h, x1[B], y[B], z[B], w[B]], {B, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + y[0]; 
     p3[j] = (h^\[Alpha]*Sum[b[j - C1]*f3[C1*h, x1[C1], y[C1], z[C1], w[C1]], {C1, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + z[0]; 
     p4[j] = (h^\[Alpha]*Sum[b[j - C2]*f4[C2*h, x[C2], y[C2], z[C2], w[C2]], {C2, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + w[0]; 
     x[j] = (1/Gamma[\[Alpha] + 2])*(h^\[Alpha]*(Sum[a[j - K]*f1[h*K, x[K], y1[K], z[K], w[K]], 
           {K, 1, j - 1}] + f1[h*j, p1[j], p2[j], p3[j], p4[j]] + 
          ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*f1[0, x[0], y[0], z[0], w[0]])) + 
       x[0]; y[j] = (1/Gamma[\[Alpha] + 2])*h^\[Alpha]*
        (Sum[a[j - K]*f2[h*K, x1[K], y[K], z[K], w[K]], {K, 1, j - 1}] + 
         f2[h*j, p1[j], p2[j], p3[j], p4[j]] + ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*
          f2[0, x[0], y[0], z[0], w[0]]) + y[0]; 
     z[j] = (1/Gamma[\[Alpha] + 2])*h^\[Alpha]*(Sum[a[j - K]*f3[h*K, x1[K], y[K], z[K], w[K]], 
          {K, 1, j - 1}] + f3[h*j, p1[j], p2[j], p3[j], p4[j]] + 
         ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*f3[0, x[0], y[0], z[0], w[0]]) + z[0]; 
     w[j] = (1/Gamma[\[Alpha] + 2])*h^\[Alpha]*(Sum[a[j - K]*f4[h*K, x[K], y[K], z[K], w[K]], 
          {K, 1, j - 1}] + f4[h*j, p1[j], p2[j], p3[j], p4[j]] + 
         ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*f4[0, x[0], y[0], z[0], w[0]]) + 
       w[0]; ]; , {s, 1, smax}]
lst1 = Table[{x[j], y[j], z[j]}, {j, n}]; lst = 
 Table[{x[j], y[j], z[j]}, {j, 10, n, 10}]; lst2 = 
 Table[{x[j], y[j]}, {j, n}];

Numerical solution with NDSolve

Clear[x, y, z, w];
sol = NDSolve[{x'[t] == f1[t, x[t], y[t - tau], z[t], w[t]], 
    y'[t] == f2[t, x[t - tau], y[t], z[t], w[t]], 
    z'[t] == f3[t, x[t - tau], y[t], z[t], w[t]], 
    w'[t] == f4[t, x[t], y[t], z[t], w[t]], x[t /; t <= 0] == x0, 
    y[t /; t <= 0] == y0, z[t /; t <= 0] == z0, 
    w[t /; t <= 0] == w0}, {x, y, z, w}, {t, 0, tmax}];

Compare two solution

{Show[ParametricPlot3D[{x[t], y[t], z[t]} /. sol[[1]], {t, .0, tmax}, 
   AxesLabel -> {x, y, z}], ListPointPlot3D[lst, PlotStyle -> Red]], 
 Show[ParametricPlot[{x[t], y[t]} /. sol[[1]], {t, .0, tmax}, 
   Frame -> True, Axes -> False, FrameLabel -> {x, y}], 
  ListPlot[lst2, PlotStyle -> Red]]}

Second, we run code for $\alpha =0.93, smax=300$ and plot numerical solution

a1 = 2.1; b1 = 0.01; 
c1 = 2.6; m1 = 8.4; m2 = 6.4; m3 = 2.2; 
f1[t_, x_, y_, z_, w_] := x*(y - a1) + z + m1*w; 
f2[t_, x_, y_, z_, w_] := -(b1*y) - x^2 + 1 + m2*w; 
f3[t_, x_, y_, z_, w_] := -(c1*z) - x + m3*w; 
f4[t_, x_, y_, z_, w_] := (-x)*y*z
\[Alpha] = 0.93; 
h = 0.01; 
x0 = 2; 
y0 = 0; 
z0 = -0.2; w0 = 0.4; tau = 0.1; tmax = 30; nn = Round[tau/h]; smax = Round[tmax/tau]; 
  n = nn*smax; Do[x[i] = x0; y[i] = y0; z[i] = z0; w[i] = w0; , {i, -nn, 0}]; 
For[k = 1, k <= n, k++, b[k] = k^\[Alpha] - (k - 1)^\[Alpha]; 
    a[k] = -(2*k^(\[Alpha] + 1)) + (k - 1)^(\[Alpha] + 1) + (k + 1)^(\[Alpha] + 1); ]; 
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn]; , {i, 0, s*nn}]; 
   For[j = (s - 1)*nn + 1, j <= s*nn, j++, 
    p1[j] = (h^\[Alpha]*Sum[b[j - A]*f1[A*h, x[A], y1[A], z[A], w[A]], {A, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + x[0]; 
     p2[j] = (h^\[Alpha]*Sum[b[j - B]*f2[B*h, x1[B], y[B], z[B], w[B]], {B, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + y[0]; 
     p3[j] = (h^\[Alpha]*Sum[b[j - C1]*f3[C1*h, x1[C1], y[C1], z[C1], w[C1]], {C1, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + z[0]; 
     p4[j] = (h^\[Alpha]*Sum[b[j - C2]*f4[C2*h, x[C2], y[C2], z[C2], w[C2]], {C2, 0, j - 1}])/
        Gamma[\[Alpha] + 1] + w[0]; 
     x[j] = (1/Gamma[\[Alpha] + 2])*(h^\[Alpha]*(Sum[a[j - K]*f1[h*K, x[K], y1[K], z[K], w[K]], 
           {K, 1, j - 1}] + f1[h*j, p1[j], p2[j], p3[j], p4[j]] + 
          ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*f1[0, x[0], y[0], z[0], w[0]])) + 
       x[0]; y[j] = (1/Gamma[\[Alpha] + 2])*h^\[Alpha]*
        (Sum[a[j - K]*f2[h*K, x1[K], y[K], z[K], w[K]], {K, 1, j - 1}] + 
         f2[h*j, p1[j], p2[j], p3[j], p4[j]] + ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*
          f2[0, x[0], y[0], z[0], w[0]]) + y[0]; 
     z[j] = (1/Gamma[\[Alpha] + 2])*h^\[Alpha]*(Sum[a[j - K]*f3[h*K, x1[K], y[K], z[K], w[K]], 
          {K, 1, j - 1}] + f3[h*j, p1[j], p2[j], p3[j], p4[j]] + 
         ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*f3[0, x[0], y[0], z[0], w[0]]) + z[0]; 
     w[j] = (1/Gamma[\[Alpha] + 2])*h^\[Alpha]*(Sum[a[j - K]*f4[h*K, x[K], y[K], z[K], w[K]], 
          {K, 1, j - 1}] + f4[h*j, p1[j], p2[j], p3[j], p4[j]] + 
         ((j - 1)^(\[Alpha] + 1) - (-\[Alpha] + j - 1)*j^\[Alpha])*f4[0, x[0], y[0], z[0], w[0]]) + 
       w[0]; ]; , {s, 1, smax}]
{ListPointPlot3D[Table[{x[j], y[j], z[j]}, {j, n}], PlotRange -> Full, 
  AxesLabel -> {"x", "y", "z"}],
 ListLinePlot[Table[{x[j], y[j]}, {j, n}], PlotRange -> Full, Frame -> True, 
  Axes -> False, FrameLabel -> {"x", "y"}, AspectRatio -> 1, 
  PlotLabel -> Row[{"[Tau] = ", tau}]]}