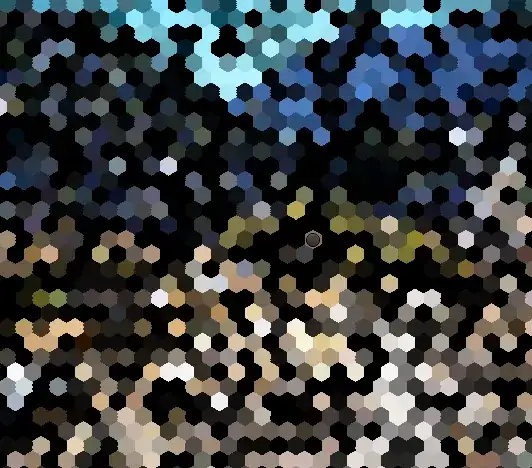How to add hexagon mosaic to a photo?

Question

I want to put a hexagon mosaic on the area of the picture (the effect is similar to the figure below):

ImageCompose[ img, 
 ImageTransformation[img, 18 Floor[#/18] + 1 &, DataRange -> Full, 
  Masking -> Rectangle[{50, 50}, {150, 150}], Padding -> Transparent]]

But the above code can only generate square mesh mosaic in the specified area. What can I do to make a hexagon mosaic?

Image used in Code:

Answer 1

It is possible to find a function that converts a pixel coordinate into a hexagon center, and recolor the image that way (i.e. similar to your ImageTransformation approach). However, when looking into it, it seemed like it could take a while to get it right. I decided to look for a solution that would be easier to implement and easier to understand, and I came up with the following.

We start by defining a function that takes an offset $(x, y)$ and a width and height, and converts that into a collection of polygons:

polygon[r_, c_, s_] := Module[{xOff, yOff},
  If[
   OddQ[c],
   yOff = 2 Cos[30 Degree] r + Cos[30 Degree],
   yOff = 2 Cos[30 Degree] r
   ];
  xOff = (1 + Sin[30 Degree]) c;
  Polygon[s (# + {xOff, yOff}) & /@ CirclePoints[6]]
  ]
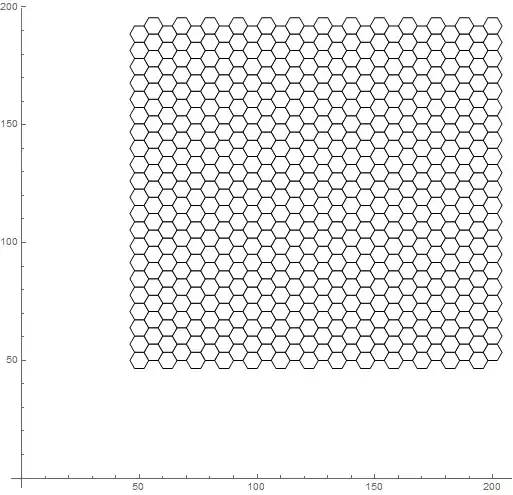
hexagonalLattice[{width_, height_}, {xOff_, yOff_}, scale_] := Module[{nx, ny},
  nx = Ceiling[width/(scale (1 + Sin[30 Degree]))];
  ny = Ceiling[height/((2 scale + 1) Cos[30 Degree])];
  Flatten@Table[Normal@Translate[polygon[r, c, scale], {xOff, yOff}], {r, 0, ny}, {c, 0, nx}]
  ]
Graphics[{
  FaceForm[White],
  EdgeForm[Black],
  hexagonalLattice[{150, 150}, {50, 50}, 4]
  },
 Axes -> True,
 AxesOrigin -> {0, 0}
 ]

Note that I attempt to convert Translate[Polygon[...]] into Polygon using Normal. This works for 3D primitives but, for unknown reasons, it does not yet work for 2D primitives. I therefore patch Normal to do this:

Unprotect[Normal];
Normal@Translate[Polygon[coords_], {xOff_, yOff_}] := Polygon[# + {xOff, yOff} & /@ coords]
Protect[Normal];

We now create a collection of polygons corresponding to the region that we want to mask, get the centroids of the polygons, and get the corresponding colors from the image. We can then use HighlightImage to draw the polygons with the correct color into the image:

img = Import["https://i.stack.imgur.com/JveCc.jpg"];
lattice = hexagonalLattice[{100, 100}, {50, 50}, 8];
centroids = RegionCentroid /@ lattice;
colors = PixelValue[img, centroids];
primitives = Transpose[{
    Directive[
       EdgeForm[None],
       Opacity[1],
       RGBColor[#]
       ] & /@ colors,
    lattice
    }];
HighlightImage[img, primitives]

Here is the same with a more detailed lattice so that it is easier to see that the color assignment works: