How to show all global minimizers?

Question

This is a follow-up to this question and I'm aware of this question for the local minimizers case.

Consider, for $0\leq \epsilon\leq 1$ and $0<q,p<1$, the function $$ \begin{align} f(\epsilon,q,p)&=\frac{(1-\epsilon)}{3}\left[\cos\left(2\pi q\right)+\cos\left(2\pi p\right)+\cos\left(2\pi\left(q+p\right)\right)\right]\nonumber\\ &\hspace{5mm}+\frac{\epsilon}{6}\bigg[\cos\left(4\pi q\right)+\cos\left(2\pi (p-q)\right) + \cos\left(4\pi p\right)\nonumber\\ &\hspace{10mm}+\cos\left(2\pi\left(2q+p\right)\right)+\cos\left(2\pi\left(q+2p\right)\right)+\cos\left(4\pi\left(q+p\right)\right) \bigg] \end{align} $$

Given, in Mathematica, as

f = Function[{e, q, p},
  ((1 - e)/3) (Cos[2 Pi q] + Cos[2 Pi p] + 
  Cos[2 Pi (q + p)]) + (e/6) (Cos[4 Pi q] + Cos[2 Pi (q - p)] + 
  Cos[4 Pi p] + Cos[2 Pi (2 q + p)] + Cos[2 Pi (q + 2 p)] + 
  Cos[4 Pi (q + p)])];

For each $\epsilon$, I want to find all (or as many as possible) global minimizing pairs $(q,p)$ of $f$. For example, following the methodology in my previous question, I can use inbuilt functions like Minimize, NMinimize or FindInstance to get some results, but I was wondering whether there is a better way. Doing so in the case $\epsilon=0$, for instance, I get the minimizing pairs $(1/3,1/3)$ and $(2/3,2/3)$ with the following code

eps = 0; n = 10;
min = NMinimize[{f[eps, q, p], 0 < q < 1 && 0 < p < 1}, {q, p}];
FindInstance[{f[eps, q, p] == N[Rationalize[min[[1]]]], 
  0 < q < 1 && 0 < p < 1}, {q, p}, n]

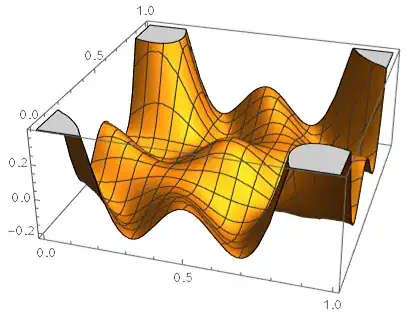
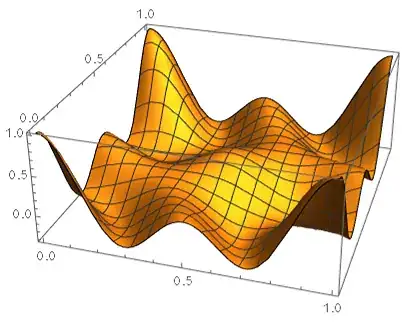
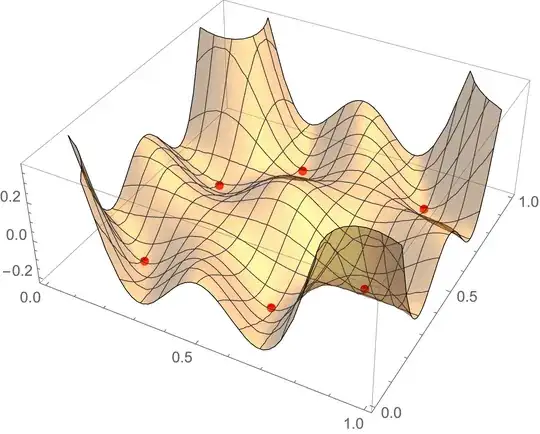
However, for other values of $\epsilon$ (for example $0.6$ and $0.8$), this fails. FindInstance does not return anything, though at least one minimizer is found is found via NMinimize. What is happening? Plotting $f$ for $0.6$ and $0.8$ seems to suggest that there are more than one global minimizers, but I can't find them

Plot3D[f[0.6, q, p], {q, 0, 1}, {p, 0, 1}]

Plot3D[f[0.8, q, p], {q, 0, 1}, {p, 0, 1}]

By doing it in the tradicional manner, that is, finding the gradient and Hessian, one could hope to get better results (though this would include local minima, if not coincident with the global minimum), and this was suggested before, but it does not seem to work as well due to some limitations of Solve or NSolve.

Any ideas?

Answer 1

Clear["Global`*"]

f = Function[{e, q, 
    p}, ((1 - e)/3) (Cos[2 Pi q] + Cos[2 Pi p] + Cos[2 Pi (q + p)]) + (e/
       6) (Cos[4 Pi q] + Cos[2 Pi (q - p)] + Cos[4 Pi p] + 
       Cos[2 Pi (2 q + p)] + Cos[2 Pi (q + 2 p)] + Cos[4 Pi (q + p)])];

{min, arg} = NMinimize[{f[6/10, q, p], 0 < q < 1, 0 < p < 1}, {q, p}]

(* {-0.220032, {q -> 0.193389, p -> 0.193389}} *)

So the global minimum must be less than -0.22

Use FindRoot to do a grid search for the critical points. Use Select to eliminate maximums. And use DeleteDuplicates to remove redundancies.

sol = DeleteDuplicates[
  Select[(FindRoot[{D[f[6/10, q, p], p] == 0, 
         D[f[6/10, q, p], q] == 0}, {{q, #[[1]]}, {p, #[[2]]}}, 
        WorkingPrecision -> 25] & /@ 
      Flatten[Outer[{#1, #2} &, Range[0, 1, 1/10], Range[0, 1, 1/10]], 
       1]), (f[6/10, q, p] /. #) < -0.22 &] /. 
   x_?NumericQ :> Round[x, 10.^-15]]
(* {{q -> 0.193389, p -> 0.193389}, {q -> 0.193389, 
  p -> 0.613221}, {q -> 0.386779, p -> 0.806611}, {q -> 0.613221, 
  p -> 0.193389}, {q -> 0.806611, p -> 0.386779}, {q -> 0.806611, 
  p -> 0.806611}} *)

Verifying,

f[6/10, q, p] /. sol
(* {-0.220032, -0.220032, -0.220032, -0.220032, -0.220032, -0.220032} *)
Show[
 Plot3D[f[6/10, q, p], {q, 0, 1}, {p, 0, 1},
  PlotStyle -> Opacity[0.4],
  ClippingStyle -> None],
 Graphics3D[{Red, AbsolutePointSize[6], Point[{q, p, f[6/10, q, p]} /. sol]}]]