How to make a 3D plot of light intensity for an image of a rectangular diffraction pattern?

Question

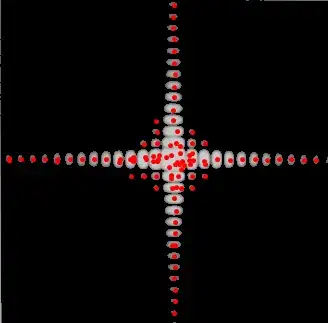
A point source of light passing through a rectangular aperture causes a diffraction pattern that is a extension of a single single diffraction pattern (In that the pattern appears in 2 axes).

The pattern that is observed is as follows:

Is it possible to create a 3D plot for the intensity of light. With the origin at the center of the diffraction pattern, from the image.

Something like this.

I know how to create a 2D intensity graph for the case of single slit diffraction. But that is using Tracker and not Mathematica. How can I make this 3D plot using Mathematica?

Also I haven't done image processing of this kind with Mathematica before. Am I supposed to pre-edit the image in any way or just use the raw image from the camera?

Thanks for any and all help.

EDIT: Another question I just thought of. How can I extract the values for intensity for the maximas from the image?

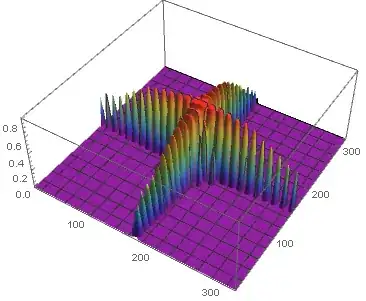
Something like ListPlot3D[ImageData[RemoveAlphaChannel@ColorConvert[img,"Grayscale"]], PlotRange -> All, ColorFunction -> "Rainbow", DataRange -> {{-50, 50}, {-50, 50}}] might be a worthwhile start? — Carl Lange, Mar 05 '21 at 13:42
This is really good. Do you know how I can get the intensity values for the maximas. I'm not sure how to extract it from the image. — Boris, Mar 06 '21 at 07:20
You should linearize colorspace in order to get real physical intencity values. More info: "The correct way to linearize colorspace before resizing, blurring etc", also see the "UPDATE" section of this answer. — Alexey Popkov, Mar 07 '21 at 12:57

score 2 · Answer 1 · answered Mar 05 '21 at 15:34

2

I took your grayscale pattern and did following:

a = ImageData@Import["https://i.stack.imgur.com/3O5xI.png"];
ListPlot3D[MovingAverage[b[[All, All, 1]], 6], 
 PlotRange -> {{10, 320}, {5, 320}, All}, 
 ColorFunction -> "Rainbow"]

The MovingAverage was used to make the background noise of your image a bit softer. The [[All,All,1]] after b were used because the initial image contains alfa-channel..

answered Mar 05 '21 at 15:34

Rom38

5,129
13
28

Does this give quantitative measurements? Any idea how I can extract out this information for the maxima values. – Boris Mar 06 '21 at 07:14
1

@BhorisDhanjal, I took your picture, man, and just have redrawn it in 3D as you ask. It is evidently not a correct physical data because zero order of diffraction is too weak . I guess, it is manually suppressed for nice view of the higher orders. You should solve the diffraction problem for your case to obtain the physically correct data about real amplitudes of orders. – Rom38 Mar 06 '21 at 08:58
Yup I'll do that thanks a lot for your help. – Boris Mar 06 '21 at 09:06
@BhorisDhanjal, actually, the simple model of diffraction for any hole can be done very easy - you just need to make a summation of complex amplitudes of spherical waves (that sit on the outer face of the slit) at the desired plane after the slit. – Rom38 Mar 06 '21 at 09:08
I have found the analytical formula for intensity of this case. Which was $I(x,y) \propto sinc^{2} \left ( \frac{\pi Wx}{\lambda z} \right ) sinc^{2} \left ( \frac{\pi Hy}{\lambda z} \right )$. However I was looking to try and verify it via observation as well. I think I can get those values for intensity using Tracker so it should be fine. – Boris Mar 06 '21 at 09:13
You can also do RemoveAlphaChannel[ColorConvert[img, "GrayScale"]] instead of b[[All, All, 1]] as I showed in my comment - it really just depends on how clear you want your code to be. – Carl Lange Mar 06 '21 at 09:58
@BhorisDhanjal, This solution is close enough to reality. The zero order should be about 5-10 times higher than the first one. However, the picture with correct ratio I1/I0 will looks too ugly and mostly it is drawn so that I0~I1. – Rom38 Mar 06 '21 at 10:17

kglr · Accepted Answer · 2021-03-06T09:19:34.187

2

image = Import["https://i.stack.imgur.com/3O5xI.png"];

intensity = First @ Values @ ComponentMeasurements[image, "IntensityData"]; 

intensityarray = ArrayReshape[intensity, Reverse @ ImageDimensions @ image];

ListPlot3D[intensityarray, ColorFunction -> "Rainbow", PlotRange -> All]

"IntensityData" seems to be the same as GrayLevel value when we remove the alpha channel from the input image and ColorConvert the image to GrayLevel:

intensityarrayb = ImageData[ColorConvert[RemoveAlphaChannel@image, GrayLevel]];
intensityarray == intensityarrayb

True

edited Mar 06 '21 at 09:19

answered Mar 06 '21 at 08:06

kglr

394,356
18
477
896

Thanks this is great! Do you know how I can get the values of intensity for each of the maixmas from that image. Also what is the unit for this intensity. I've tried searching online I can't seem to find it. – Boris Mar 06 '21 at 08:45
@BhorisDhanjal, "IntensityData" for a pixel seems to be gray level value (a value b/w 0 and 1). Yoy can use MaxDetect on intensityarray (e.g., MaxDetect[intensityarray, .1] //Colorize) to identify the local maximas. – kglr Mar 06 '21 at 09:32

score 1 · Answer 3 · answered Mar 06 '21 at 17:27

For quantitative measurements mentioned in comments of previois answers:

i = Import["https://i.stack.imgur.com/dYVTC.png"]

Not a great attempt at cleaning up the image:

i0 = Rasterize[RemoveBackground[RemoveBackground[ImageMultiply[i, MaxDetect[i, 0.6]]], Black],Background -> Black]

You can identify all the max intenisty points of each section:

markers = MaxDetect[i0, Padding -> 1];
HighlightImage[i0, markers, Method -> {"DiskMarkers", 5}]

Measure the max intesity of each segment:

ComponentMeasurements[i0, "MaxIntensity"]

If you explore ComponentMeasurements[] there is a bunch of nice stuff you can measure and plot.

out[1]: {1 -> 0.407843, 2 -> 0.372549, 3 -> 0.380392,...}

Stealing Rom38's 3D code:

a = ImageData@i0;
ListPlot3D[MovingAverage[a[[All, All, 1]], 6], 
 PlotRange -> {{10, 320}, {5, 320}, All}, ColorFunction -> "Rainbow"]

I think you can use a median filter like this, if you would like a smoother graph as in your original post

Smoothing the Sharp Undesired Points in ListPlot3D

How to make a 3D plot of light intensity for an image of a rectangular diffraction pattern?

3 Answers3