2

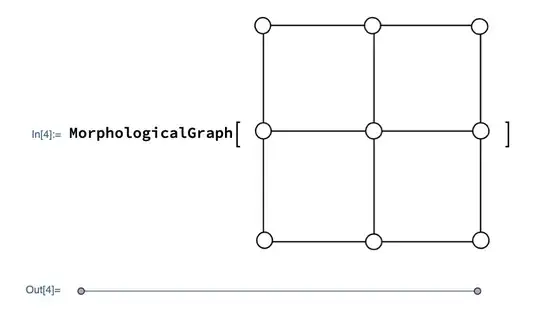
I'm trying to use MorphologicalGrpah to produce a graph, but I tried with a different graph. It does not print the exact graph. Is there a way to fix it? Is there a program where I can draw a graph by my hand and convert it to Wolfram Language?

enter image description here

Mubarak Alsaeedi
  • 235
  • 1
  • 9
  • 2
    I am commenting on the OP because this addresses comments made in the two current answers: perhaps you may consider the value that would come with learning how to produce these graphs using the Wolfram Language, rather than trying to use the methods you are currently attempting. This is, in its current state, a problem of image recognition. If you continue down this path, you may find value in training a neural network to produce your desired outcome. This too can be done with the Wolfram Language. – CA Trevillian Mar 07 '21 at 09:46

4 Answers4

5
img = Import["https://i.stack.imgur.com/g4Z5W.png"]

enter image description here

We can identify the circles representing vertices and remove them and fill the spaces of removed vertices to get an image to pass to MorphologicalGraph:

img2 = Colorize @ DeleteBorderComponents @ MorphologicalComponents @ Binarize @ img

enter image description here

img3 = DeleteSmallComponents[img2, 500]

enter image description here

img4 = Binarize @ RemoveBackground @ ColorNegate @ img3

enter image description here

img5 = ColorNegate @ MorphologicalTransform[img4, "BoundingBoxes", Infinity]

enter image description here

MorphologicalGraph[img5, VertexSize -> Small]

enter image description here

Note: The magic number 500 in step 3 is obtained by squinting at the "Area", "Circularity" and "Rectangularity" numbers for the 13 components of img2:

ComponentMeasurements[img2, {"Area", "Circularity", "Rectangularity"}]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
5

If you are determined to work from the way the graph has been drawn, then you need to modify the input image to get it into a form MorphologicalGraph can work with. This is one way of doing it - the idea is to fill in the circles where the vertices are then use Thinning:

img=enter image description here

Then (the value of 'r' arrived at from experiment):

With[{r = 12}, TopHatTransform[img, DiskMatrix[r]]] // Binarize // Erosion[#, 2] &;
ComponentMeasurements[%, "Mask", And[#Count > 200, .9 < #Circularity < 1.1] &, "ComponentAssociation"]//Binarize;
infill = ImageAdd[Image /@ % // Values]

enter image description here

Now add this back to the negation of the original image to fill in the disks:

filled = ImageAdd[ColorNegate[img] // Binarize, Dilation[infill, 3]]

enter image description here

Then use Thinning:

thinned = Thinning[filled]

enter image description here

Finally, MorphologicalGraph:

MorphologicalGraph[thinned]

enter image description here

EstabanW
  • 700
  • 1
  • 4
  • 11
  • Thank you. If I want to follow this procedure to other graphs, I just need to fix the "r" value? Another way to say it, can I use this procedure for any graph I see in a textbook? – Mubarak Alsaeedi Mar 07 '21 at 11:24
  • 1
    @MubarakAlsaeedi no, the procedure I've shown works for the form of input image you showed, it won't generalise to "any" graph in a textbook, there are no end of ways graphs can be drawn. – EstabanW Mar 07 '21 at 11:56
3

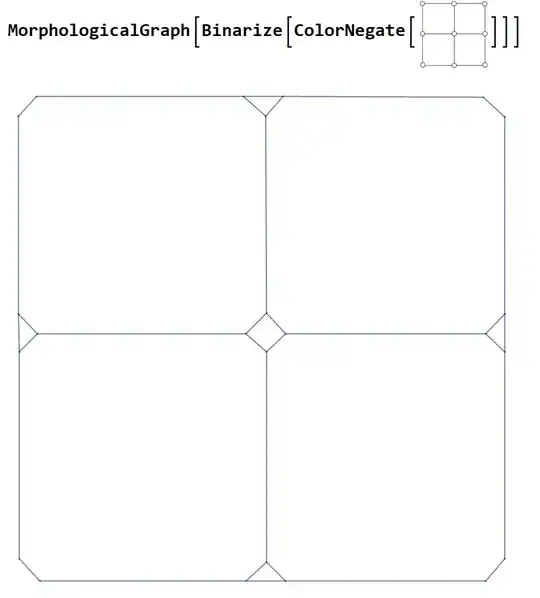
As per the "Applications" section of the documentation, you can use ColorNegate:

enter image description here

As per your comment: if you want to get Daniel Huber's graph from your image, try MorphologicalGraph[ColorNegate@Binarize@Erosion[i, DiskMatrix[20]]] where i is the image.

enter image description here

anderstood
  • 14,301
  • 2
  • 29
  • 80
  • It's good, but that does not give me the desired graph. The original graph has 9 vertices, but the graph you obtained has 24 Vertex. – Mubarak Alsaeedi Mar 07 '21 at 08:20
  • @MubarakAlsaeedi Why don't you draw your graph in such a way that it is compatible with MorphologicalGraph? Clearly, the purpose of MorphologicalGraph is not to recognize arbitrarily-styles hand-drawn graphs, but to extract a graph from a branching structure. – Szabolcs Mar 07 '21 at 08:44
  • @Szabolcs I can do that, but I'm searching for a way to convert an image to a graph. I'm currently studying a textbook with lots of graphs, and I want to insert them in Mathematica so I can play with them by capturing the graph and insert it as an image and then convert them to a graph. – Mubarak Alsaeedi Mar 07 '21 at 08:49
3

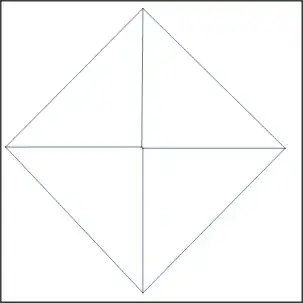
The circles in your drawing are recognized as branch point. Therefore, do not draw circles.

Here is an example picture:

enter image description here

With this pictures stored in im:

im = ColorNegate[im]
MorphologicalGraph[im]

We get the following graph:

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
  • Great, thank you. One last question, is there a way when I study graphs in mathematics textbooks, I can capture them then convert them in Mathematica without drowning them without circles? – Mubarak Alsaeedi Mar 07 '21 at 09:23
  • I am using: https://duckcapture.de.softonic.com/ – Daniel Huber Mar 07 '21 at 09:31
  • thank you, I’m using Mac to capture easily; what I’m searching for is software like Mathpix (a software convert equations to LaTeX), but I want a software convert image to graph. – Mubarak Alsaeedi Mar 07 '21 at 09:39