I have an expression:
chisq[f_, x_, y_, e_, pars__] := Sum[((y[k] - f@@Join[{x[k]},pars])/e[k])^2, {k,1,n}]
which should work for any function that has x as an argument, as well as some arbitrary number of parameters. Say, if I have a and b, chisq[f,x,y,e,{a,b}] will give
which is just an expression of chi-square $\chi^2$ for a set of data $\{x_i, y_i\pm e_i\}_{i=1}^{n}$ against a model described by f[x,a,b].
What I want to do is calculate $\nabla\chi^2 $ to solve $\nabla \chi^2=0$ . If I take derivative against a, D[chisq[f,x,y,e,{a,b}],a], the result is
which is not technically wrong. But I want to arrange this into a format so that it could be solved, by extracting the multiplicative constants out of the summation and splitting the summation into pieces. For example, Simplify[D[chisq[f,x,y,e,{a,b}],a]/2] gives
which has 2 in all of its terms but does not get it out of the sum. What I want it to happen is something like $$ \chi^2 = \sum_{i=1}^{N} \frac{\left(y_i - f(x_i;a,b)\right)^2}{{e_i}^2} \\ \frac{\partial}{\partial a}\chi^2 = 2 \left[\sum_{i=1}^{N} \frac{f(x_i;a,b) \partial_a f(x_i;a,b) - y_i \partial_a f(x_i;a,b)}{{e_i}^2}\right] \\ = 2 \sum_{i=1}^{N} \frac{f(x_i;a,b) \partial_a f(x_i;a,b)}{{e_i}^2} - 2 \sum_{i=1}^{N} \frac{y_i \partial_a f(x_i;a,b)}{{e_i}^2} $$
For example, it should work for linear fit $f(x;a,b) = a+bx$,
$$ \chi^2 = \sum_{i=1}^{N} \frac{\left(y_i - a - b x_i\right)^2}{{e_i}^2} \\ \frac{\partial}{\partial a}\chi^2 = 2 \left[\sum_{i=1}^{N} \frac{a+b x_i}{{e_i}^2} - \sum_{i=1}^{N} \frac{y_i}{{e_i}^2}\right] = 2 \left[a \sum_{i=1}^{N} \frac{1}{{e_i}^2} + b \sum_{i=1}^{N} \frac{x_i}{{e_i}^2} - \sum_{i=1}^{N} \frac{y_i}{{e_i}^2}\right] \\ \frac{\partial}{\partial b}\chi^2 = 2 \left[\sum_{i=1}^{N} \frac{\left(a+b x_i\right) x_i}{{e_i}^2} - \sum_{i=1}^{N} \frac{y_i x_i}{{e_i}^2}\right] = 2 \left[a \sum_{i=1}^{N} \frac{ x_i}{{e_i}^2} + b \sum_{i=1}^{N} \frac{{x_i}^2}{{e_i}^2} - \sum_{i=1}^{N} \frac{y_i x_i}{{e_i}^2}\right] $$
and so on. How can I make the sum D[chisq[f,x,y,e,{a,b}],a] to be expanded like this?
Edit: I've narrowed down the problem, but not out of the woods yet.
I think I'm halfway there. Thanks to a post https://mathematica.stackexchange.com/a/199464/29247 and with a lot of experimentation, I somehow got hold of some set of rules, which could do what I want when successively applied several times.
First, the one from aforementioned post
Sum[Times[Longest[u___], x_] , {y_, z___}] :>
Times[u] Sum[Times[x], {y, z}] /;(FreeQ[{u}, y])
can extract multiplicative factor.
Second,
Sum[Plus[ Longest[u___], x_] , {y_, z___}] :> Plus[Sum[u, {y, z}], Sum[x, {y, z}]]
will split the summation.
Third,
Times[Plus[Longest[u___], v_],x_] :> Times[Plus[u], x] + Times[v, x]
is used for expanding the fraction, since when it's multiplied with common factor, it is not recognized by two rules above.
So, for instance,
Sum[(a[k] + q b[k])/(c[k]), {k,1,n}] /.
Times[Plus[Longest[u___], v_],x_] :> Times[Plus[u], x] + Times[v, x] /.
Sum[Plus[ Longest[u___], x_] , {y_, z___}] :> Plus[Sum[u, {y, z}], Sum[x, {y, z}]] /.
Sum[Times[Longest[u___], x_] , {y_, z___}] :> Times[u] Sum[Times[x], {y, z}] /;(FreeQ[{u}, y])
I get what I want:
But if I make it a set of rules then apply,
Sum[(a[k] + q b[k])/(c[k]), {k,1,n}] //. {
Times[Plus[Longest[u___], v_],x_] :> Times[Plus[u], x] + Times[v, x] ,
Sum[Plus[ Longest[u___], x_] , {y_, z___}] :> Plus[Sum[u, {y, z}], Sum[x, {y, z}]] ,
Sum[Times[Longest[u___], x_] , {y_, z___}] :> Times[u] Sum[Times[x], {y, z}] /;(FreeQ[{u}, y])
}
I get
I figured that it seems the rule from the aforementioned post
Sum[Times[Longest[u___], x_] , {y_, z___}] :>
Times[u] Sum[Times[x], {y, z}] /;(FreeQ[{u}, y])
is causing this problem. If I remove it from the rules and apply separately, it seems to work as intended. But I don't understand this behavior. I mean, I'm novice in terms of Wolfram Language, and I understand almost none of what is happening. So, could someone explain why this isn't working, and what I should do to make it work as a single list of rules?


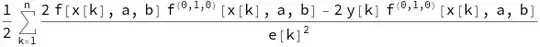

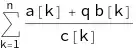
f[x_, a_, b_] := a*x + b;, thenD[chisq[f, x, y, e, {a, b}], a]results in $$\sum _{k=1}^n \frac{2 a x(k)^2+2 b x(k)-2 x(k) y(k)}{e(k)^2} .$$ Why do you dislike it? As far as I remember it, there are some tricks to extract2outside the sum. – user64494 Mar 10 '21 at 09:55aandbas well, since they don't explicitly depend on the iterative index of the sum. – Hojin Cho Mar 11 '21 at 00:05Solve[D[chisq[f, x, y, e, {a, b}, a]==0, a]orSolve[{D[chisq[f, x, y, e, {a, b}, a]==0, D[chisq[f, x, y, e, {a, b}, b]==0}, {a,b}]. – Hojin Cho Mar 11 '21 at 00:46