23

I am getting these results:

0.999999999999988 < 1.0  (*False*)
0.999999999999988 >=  1.0  (*True*)
0.999999999999988 ===  1.0  (*False*)

Block[{$MinPrecision = $MachinePrecision, $MaxPrecision=$MachinePrecision}, 0.999999999999988 >=  1.0] (False)


N[0.999999999999988 -  1.0]  (small negative number, but larger in magnitude than machine precision)


PossibleZeroQ[N[0.999999999999988 -  1.0]]  (False)

Is there a workaround?

amWhy
  • 103
  • 2
Craig Carter
  • 4,416
  • 16
  • 28
  • I think you found the work around: instead of testing a == b, check a - b == 0 (same with <, >). The normal rules of arithmetic don't necessarily apply when you're working with floating point numbers. – Brett Champion Mar 15 '21 at 16:27
  • 2
    0.999999999999988`17. >= 1.`17. gives False See also Possible Issues in the documentation of Equal. – Rolf Mertig Mar 15 '21 at 16:27
  • 1
    Finding that this was the source of a larger problem was a (time-consuming) surprise. I think that including this in Possible Issues for Less would be helpful, or perhaps an option for Less[a,b,NumericalPrecision->xxx]? – Craig Carter Mar 15 '21 at 16:51
  • 1
    Related/duplicate: (48810), (132890) – Michael E2 Mar 15 '21 at 20:40
  • Oh, I was looking in the docs at LessThan (where "Possible Issues" is absent). I see it in Less now. Thanks. – Craig Carter Mar 15 '21 at 20:47
  • Note that while 0.999999999999988 === 1.0 gives False, 0.999999999999988 == 1.0 gives True. === is SameQ, and == is Equal; SameQ tests if they're literally the same expression, whereas Equal cooperates with <=. (Edit: Oops, saw this was covered in one of the not-accepted answers, but I'll leave it here for quick reference by anyone reading this.) – thorimur Mar 16 '21 at 00:15

3 Answers3

26

You can lower the value of Internal`$EqualTolerance:

Block[{Internal`$EqualTolerance = 0},
  0.999999999999988 >= 1.0 
]

False

This can lead to unexpected behaviors too:

Block[{Internal`$EqualTolerance = 0},
  0.1 + 0.2 == 0.3 
]

False

Maybe there's a better sweet spot that fits your needs. For these two examples, this works:

Block[{Internal`$EqualTolerance = Internal`$SameQTolerance},
  0.999999999999988 >= 1.0 
]

False

Block[{Internal`$EqualTolerance = Internal`$SameQTolerance},
  0.1 + 0.2 == 0.3 
]

True

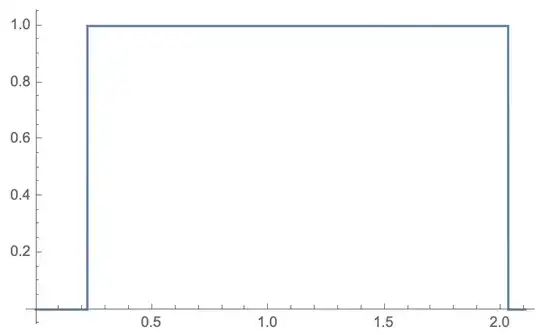
If you have a nice representative sample of values you're comparing, you can estimate a value for Internal`$EqualTolerance by plotting. These two examples return correct comparisons for values between Log10[5/3] and Log10[108]:

correctEquals[x_?NumericQ] := 
  Block[{Internal`$EqualTolerance = x}, 
    Boole[Not[0.999999999999988 >= 1.0] && (0.1 + 0.2 == 0.3)]
  ]

Plot[correctEquals[x], {x, 0, Internal`$EqualTolerance}]

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136
  • This would be a great addition to the Documentation or in a Guide. Excellent answer. – Craig Carter Mar 15 '21 at 17:32
  • 1
    This explains why 0.999999999999988 >= 1.0 was true, but it doesn't explain why 0.999999999999988 === 1.0 was simultaneously false. – BlueRaja - Danny Pflughoeft Mar 16 '21 at 03:19
  • 1
    @BlueRaja-DannyPflughoeft : "SameQ requires exact correspondence between expressions, except that it still considers Real numbers equal if they differ in their last binary digit." and RealDigits[#, 2] & /@ {0.999999999999988, 1.0} exhibits discrepancy long before the last binary digit. If you meant 0.999999999999988 == 1.0, at least on M'ma 11.3, this gives True. – Eric Towers Mar 16 '21 at 04:20
  • 1
    Any insight as to why the values that work in this case are exactly Log10[5/3] and Log10[108] ? – Carmeister Mar 16 '21 at 16:46
  • Good question, I'm curious to know why too. – Greg Hurst Mar 16 '21 at 18:13
  • @Carmeister Exactly at what Internal\$EqualTolerance` level? – wizzwizz4 Mar 16 '21 at 18:13
11

From the help.

Equal (==): Approximate numbers with machine precision or higher are considered equal if they differ in at most their last seven binary digits (roughly their last two decimal digits).

This explains the fist two cases: 0.999999999999988 and 1. differ by less than 7 digits.

SameQ (===): SameQ requires exact correspondence between expressions, except that it still considers Real numbers equal if they differ in their last binary digit.

As 0.999999999999988 and 1. differ by more than one digits they, are considered different.

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
4
Sign[ 0.999999999999988 - 1.0]

-1

user64494
  • 26,149
  • 4
  • 27
  • 56
  • 2
    This approach has its limitations: for example, following the documentation, Block[{$MaxExtraPrecision = 10000}, N[Sign[0.9999999999999999999999 - 1.0], 40]] produces 0. – user64494 Mar 15 '21 at 17:42