Fit ellipse to a arbitrary 2D image to extract centroid, orientation, major, minor axis

Question

I am wondering if there is an easy way to fit an ellipse into an arbitrary 2D image quickly, so its centroid, orientation, major, and minor axis length can directly be extracted. In MATLAB, this can be done using regionprops command quickly as shown in the following URL:

https://www.mathworks.com/matlabcentral/answers/495720-how-to-fit-an-ellipse-to-an-image-in-matlab

Do any answers from https://mathematica.stackexchange.com/questions/25589/how-can-i-detect-an-ellipse-in-a-photo?rq=1 work? — Adam, Mar 17 '21 at 04:55
Thanks, Adam! I looked at it as well, but it did not apply to what I am looking for. — fdjutant, Mar 17 '21 at 16:14

score 9 · Accepted Answer · answered Mar 17 '21 at 05:09

The similar command in MMA is ComponentMeasurement. It lists all detected bright components of an image with desired parameter.

a = Import[
  "https://www.mathworks.com/matlabcentral/answers/uploaded_files/\
253610/diskimage1.jpeg"];
cm = ComponentMeasurements[
  Binarize@a, {"Centroid", "SemiAxes", "Orientation"}]

{1 -> {{488.496, 386.124}, {750.908, 620.778}, 3.14156},
2 -> {{438.5, 868.5}, {3.66324, 2.63965}, -1.5708},
3 -> {{526.5, 868.87}, {3.31766, 2.55314}, -1.5708},
4 -> {{539., 871.}, {2.23607, 1.}, 3.14159},
5 -> {{513.864, 866.591}, {2.17306, 1.53368}, -2.87856},
6 -> {{499.6, 483.975}, {205.184, 190.328}, -0.834907},
7 -> {{349.5, 626.}, {1., 0.5}, -1.5708}}

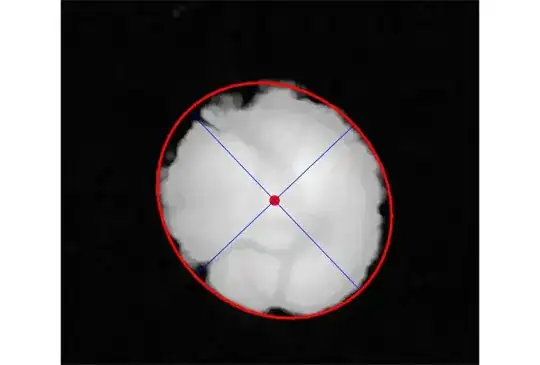
The result contains more than one entry because the presence of the caption on top of the image together with white frame. The needed spot is number six (with second biggest value of simiaxes).

Show[Binarize@a,
 Epilog -> {
   Red,
   Rotate[
    Circle[cm[[6, 2, 1]], cm[[6, 2, 2]]], 
    cm[[6, 2, 3]]]
   },
 ImageSize -> Automatic]

This is awesome! Thank you so much. – fdjutant Mar 17 '21 at 16:12 — fdjutant, Mar 17 '21 at 16:12

cvgmt · Answer 2 · 2021-03-17T06:42:37.560

Relate Determine and plot major and minor axes of ellipse

We first trim the picture to remove the label, then we use RemoveBackground,and ImageMesh to generate the mesh.

Finally we use BoundingRegion to find the minimal ellipsoid and use Eigensystem to determinate the center and major and minor.(Thanks @J. M.'s ennui)

pic = Import[
   "https://www.mathworks.com/matlabcentral/answers/uploaded_files/\
253610/diskimage1.jpeg"];
trimpic = ImageTake[pic, {40, 700}];
mesh = ImageMesh@RemoveBackground@trimpic;
ellipsoid = BoundingRegion[mesh, "MinEllipse"];
center = ellipsoid // First;
{vals, vecs} = Eigensystem[ellipsoid // Last];
{a, b} = Sqrt[vals];
major = {center - a vecs[[1]], center + a vecs[[1]]};
minor = {center - b vecs[[2]], center + b vecs[[2]]};
Show[trimpic, 
 Graphics[{{Red, PointSize[Large], Point@center, Blue, 
    Line[{major, minor}]}}], 
 Region[RegionBoundary[ellipsoid], 
  BaseStyle -> {AbsoluteThickness[2], Red}]]

This is great! I learn many commands for Mathematica image processing from your answer. — fdjutant, Mar 17 '21 at 16:13

Fit ellipse to a arbitrary 2D image to extract centroid, orientation, major, minor axis

2 Answers2