Animating a random walk of 3D water molecules?

Question

Inspired by David G. Stork’s post https://mathematica.stackexchange.com/a/84097/10361, I tried to have the molecules perform a random walk

xt = Accumulate[Prepend[RandomReal[{-1, 1}, {200, 30, 3}], RandomReal[{-5, 5}, {30, 3}]]];

like so:

h[x_] := Translate[Rotate[First@ChemicalData["Water", "MoleculePlot"],RandomReal[{0, \[Pi]}], {8, .5, 0}], x];
an[t_] :=Graphics3D[h[100*xt[[t]]],PlotRange -> {{-1000, 1000}, {-1000, 1000}, {-1000, 1000}}];
Animate[an[n], {n, 1, 100, 1}]

It works, but all the molecules have the same orientation at any time, and I think I see why, but I am not sure how to work around it. (I.e., to give them random rotations individually at each step). Any good ideas?

A more realistic, but more complicated approach, would be: Start with random positions and give every molecule a random (or better: Boltzmann distributed) velocity and a random (or better: Boltzmann distributed) angular velocity . Then propagate until 2 molecules have a distance less than some threshold. Then give these 2 molecules new velocities and angular velocities under the restriction of momentum and angular momentum conservation. For a start, you may only implement translation and add rotation if this works. — Daniel Huber, Mar 18 '21 at 11:19
It is already adequate for a coarse grained description of translational diffusion, and how it is actually often done in practice in e.g. stat. mech. Anyway, this is just for fancy ppt visualization. Thanks! — Sooner, Mar 18 '21 at 13:50

Jason B. · Accepted Answer · 2021-03-18T12:57:10.997

all the molecules have the same orientation at any time, and I think I see why

Because at each timestep you are are computing only a single angle and using it to rotate every molecule.

In this approach I use NestList to accumulate a list of TransformationFunction objects. The key here is that Composition[TransformationFunction[..], TransformationFunction[...]] will evaluate to a single transformation. So at each step I take the previous transformation and compose it with a random translation and a random rotation.

randomInitialTransform[] := Composition[
    TranslationTransform[RandomReal[{-5, 5}, 3]],
    RotationTransform[RandomReal @ {-Pi, Pi}, RandomReal[{-1,1}, 3]]
];
randomStep[inputTransform_] := Composition[
    (*small random translation*)
    TranslationTransform @ RandomReal[{-0.1, 0.1}, 3],
    (*small random rotation*)
    RotationTransform[RandomReal @ {-0.1, 0.1}, RandomReal[{-1,1}, 3]],
    inputTransform
]
randomTrajectory[n_] := NestList[randomStep, randomInitialTransform[], n];

Now make a table of trajectories, and grab the GraphicsComplex from a molecule plot:

trajectoryList = Table[randomTrajectory @ 200, 30];
graphicsComplex = First @ MoleculePlot3D[Molecule @ "water", PlotTheme -> "Tubes"];

The next part is to use GeometricTransformation, and give a list of transforms as the second argument. For example to visualize all steps of a single trajectory use

Graphics3D[GeometricTransformation[graphicsComplex, randomTrajectory[200]]]

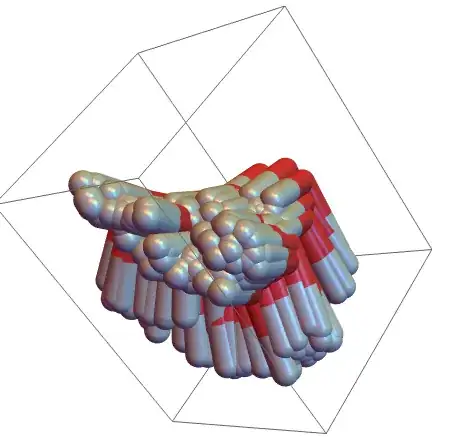
To visualize a snapshot of the ensemble use something like

snapShot[n_] := Graphics3D[
    GeometricTransformation[graphicsComplex, trajectoryList[[All, n]]],
    PlotRange -> {{-6, 6}, {-6, 6}, {-6, 6}}
]

It works with Export but not with Animate. Which is good enough for me. Also, in Version 11.0, had to use graphicsComplex = Scale[First@ChemicalData["Water", "MoleculePlot"], 0.005]; — Sooner, Mar 18 '21 at 13:52

Animating a random walk of 3D water molecules?

1 Answers1

Linked