Solving PDE with prescribed rectangular mesh

Question

Question: I want to solve a PDE using NDEigensystem. The region is a rectangle Rectangle[{0,-70}, {20, 70}]. How can I make a mesh that satisfies the following two conditions?

(1) The mesh is finer near $y \approx 0$.

(2) The line $y=0$ should be the boundary of the mesh.

Motivation: The PDE that I want to solve can be written in the following command: First, I set the mesh as below:

mesh = ToElementMesh[Rectangle[{0, -70}, {20, 70}],  
  MeshRefinementFunction -> 
   Function[{vertices, area}, 
    Block[ {x, y}, {x, y} = Mean[vertices]; 
     If[-10 < y < 10, area > 0.1, area > 10]]] ]

and then write down the PDE:

NDEigensystem[{{3*psi3[x, y] - 10*psi2[x, y]*Sign[y] - Derivative[0, 1][psi2][x, y] - 
    I*Derivative[1, 0][psi2][x, y], 3*psi4[x, y] - 10*psi1[x, y]*Sign[y] + Derivative[0, 1][psi1][x, y] - 
    I*Derivative[1, 0][psi1][x, y], 3*psi1[x, y] - 10*psi4[x, y]*Sign[y] - Derivative[0, 1][psi4][x, y] - 
    I*Derivative[1, 0][psi4][x, y], 3*psi2[x, y] - 10*psi3[x, y]*Sign[y] + Derivative[0, 1][psi3][x, y] - 
    I*Derivative[1, 0][psi3][x, y]}, PeriodicBoundaryCondition[psi1[x, y], x == 0, 
   TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], PeriodicBoundaryCondition[psi2[x, y], x == 0, 
   TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], PeriodicBoundaryCondition[psi3[x, y], x == 0, 
   TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], PeriodicBoundaryCondition[psi4[x, y], x == 0, 
   TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], DirichletCondition[psi1[x, y] == 0, 
   0 < x < 20 && (y == 70 || y == -70)], DirichletCondition[psi2[x, y] == 0, 
   0 < x < 20 && (y == 70 || y == -70)], DirichletCondition[psi3[x, y] == 0, 
   0 < x < 20 && (y == 70 || y == -70)], DirichletCondition[psi4[x, y] == 0, 
   0 < x < 20 && (y == 70 || y == -70)]}, {psi1, psi2, psi3, psi4}, Element[{x, y}, mesh], 10]

The single important fact about the PDE is that the differential operator contains $\mathrm{sgn}(y)$, hence it is not continuous at $y=0$. This is why I want the mesh boundary to include $y=0$. The mesh I created is visualized as follows:

As wanted, the mesh is finer. However, $y=0$ is not the boundary of the mesh.

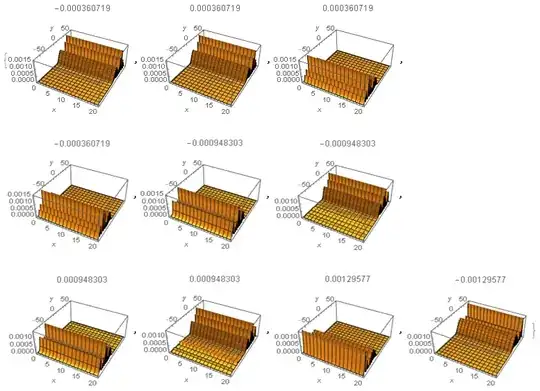
The result of one solution obtained by solving the PDE is plotted as below:

In the above plot, the horizontal direction is the $x$-direction. Note that the solution is localized near $y\approx 0$. This is why I want to make the mesh finer near $y\approx 0$. I don't believe the result is the good representation of the solution, since the graph looks jagged, which I don't expect since the differential operator has a translation symmetry in $x$-direction.

Answer 1

You can achieve your objectives with an anisotropic quad mesh that you construct manually. There are no diffusive terms in your operators, so NDEigensystem will complain about the system being convection dominated. Therefore, you may want to take a closer look at your system of equations and see if there is an opportunity to add diffusive terms.

Helper functions

The following helper functions will help construct an anisotropic Quad mesh (note that not all functions will be used).

(*Import required FEM package*)
Needs["NDSolve`FEM`"];
(*Define Some Helper Functions For Structured Meshes*)
pointsToMesh[data_] := 
  MeshRegion[Transpose[{data}], 
   Line@Table[{i, i + 1}, {i, Length[data] - 1}]];
unitMeshGrowth[n_, r_] := 
 Table[(r^(j/(-1 + n)) - 1.)/(r - 1.), {j, 0, n - 1}]
meshGrowth[x0_, xf_, n_, r_] := (xf - x0) unitMeshGrowth[n, r] + x0
firstElmHeight[x0_, xf_, n_, r_] := 
 Abs@First@Differences@meshGrowth[x0, xf, n, r]
lastElmHeight[x0_, xf_, n_, r_] := 
 Abs@Last@Differences@meshGrowth[x0, xf, n, r]
findGrowthRate[x0_, xf_, n_, fElm_] :=(*Quiet@*)
 Abs@FindRoot[
    firstElmHeight[x0, xf, n, r] - fElm, {r, 0.00000001, 
     100000000/fElm}, Method -> "Brent"][[1, 2]]
meshGrowthByElm[x0_, xf_, n_, fElm_] := 
 N@Sort@Chop@meshGrowth[x0, xf, n, findGrowthRate[x0, xf, n, fElm]]
meshGrowthByElm0[len_, n_, fElm_] := meshGrowthByElm[0, len, n, fElm]
flipSegment[l_] := (#1 - #2) & @@ {First[#], #} &@Reverse[l];
leftSegmentGrowth[len_, n_, fElm_] := meshGrowthByElm0[len, n, fElm]
rightSegmentGrowth[len_, n_, fElm_] := 
 Module[{seg}, seg = leftSegmentGrowth[len, n, fElm];
  flipSegment[seg]]
reflectRight[pts_] := 
 With[{rt = ReflectionTransform[{1}, {Last@pts}]}, 
  Union[pts, Flatten[rt /@ Partition[pts, 1]]]]
reflectLeft[pts_] := 
 With[{rt = ReflectionTransform[{-1}, {First@pts}]}, 
  Union[pts, Flatten[rt /@ Partition[pts, 1]]]]
extendMesh[mesh_, newmesh_] := Union[mesh, Max@mesh + newmesh]

Construct anisotropic Quad mesh

The following workflow will create a symmetric graded mesh about $y=0$ and a uniform mesh in the x-direction.

ht = 140;
len = 20;
ny = 100;
nx = 100;
Print["Mesh along the X-direction"]
rh = pointsToMesh@Subdivide[0, len, nx]
Print["Mesh along the Y-direction"]
rv = pointsToMesh@reflectLeft@leftSegmentGrowth[ht/2, ny/2, ht/2/ny/10]
(*Create 2D mesh with RegionProduct*)
rp = RegionProduct[rh, rv];
(* Build mesh based on region product *)
crd = MeshCoordinates[rp];
inc = Delete[0] /@ MeshCells[rp, 2];
mesh = ToElementMesh["Coordinates" -> crd, 
   "MeshElements" -> {QuadElement[inc]}];
Print["Mesh zoomed in around y=0"]
Show[mesh["Wireframe"], PlotRange -> {{0, 20}, {-5, 5}}]

This mesh is refined and has a line about $y=0$.

Solve and plot solution

(*Solve and plot*)
{vals, funs} = 
  NDEigensystem[{{3*psi3[x, y] - 10*psi2[x, y]*Sign[y] - 
      Derivative[0, 1][psi2][x, y] - I*Derivative[1, 0][psi2][x, y], 
     3*psi4[x, y] - 10*psi1[x, y]*Sign[y] + 
      Derivative[0, 1][psi1][x, y] - I*Derivative[1, 0][psi1][x, y], 
     3*psi1[x, y] - 10*psi4[x, y]*Sign[y] - 
      Derivative[0, 1][psi4][x, y] - I*Derivative[1, 0][psi4][x, y], 
     3*psi2[x, y] - 10*psi3[x, y]*Sign[y] + 
      Derivative[0, 1][psi3][x, y] - I*Derivative[1, 0][psi3][x, y]}, 
    PeriodicBoundaryCondition[psi1[x, y], x == 0, 
     TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], 
    PeriodicBoundaryCondition[psi2[x, y], x == 0, 
     TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], 
    PeriodicBoundaryCondition[psi3[x, y], x == 0, 
     TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], 
    PeriodicBoundaryCondition[psi4[x, y], x == 0, 
     TransformationFunction[{{1, 0, 20}, {0, 1, 0}, {0, 0, 1}}]], 
    DirichletCondition[psi1[x, y] == 0, 
     0 < x < 20 && (y == 70 || y == -70)], 
    DirichletCondition[psi2[x, y] == 0, 
     0 < x < 20 && (y == 70 || y == -70)], 
    DirichletCondition[psi3[x, y] == 0, 
     0 < x < 20 && (y == 70 || y == -70)], 
    DirichletCondition[psi4[x, y] == 0, 
     0 < x < 20 && (y == 70 || y == -70)]}, {psi1, psi2, psi3, psi4}, 
   Element[{x, y}, mesh], 10];
Table[Plot3D[
  funs[[i, 1]][x, y] Conjugate[funs[[i, 1]][x, y]], {x, y} \[Element] 
   mesh, PlotRange -> All, PlotLabel -> Chop@vals[[i]], Axes -> True, 
  AxesLabel -> Automatic], {i, Length[vals]}]

The solution no longer is jagged in the X-direction. However, there are many oscillations in the Y-direction. You may need to consider diffusive terms to dampen these oscillations.