We know from special relativity that:$$E^2=m_0^2c^2+p^2c^4$$$$E=\sqrt{m_0^2c^2+p^2c^4}$$$$p=m_0v$$$$E=m_0^2c^2(1+v^2)^{1/2}$$Now I know that I can use a Taylor Series to approximate the square root term when $v\ll c$:$$(1+x)^\alpha=(1+\alpha x)$$So, on paper, I can substitute in $x=v^2$ and $\alpha=\frac{1}{2}$, to get this approximation (when $v \ll c$):$$E=m_0^2c^2(1+\frac{1}{2}v^2)$$$$E=m_0^2c^2+\frac{1}{2}m_0^2c^2v^2$$Is there a clever way that I can do employ a Taylor Series in Mathematica to make the estimation for me, or do I just have to substitute by hand?
Expand[E /. Sqrt[1 + v^2] -> 1 + 1/2 v^2]
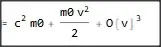
Series? – MarcoB Mar 20 '21 at 20:27ee = m0^2 c^2 Sqrt[1 + v^2]; Series[ee, {v, 0, 2}]? – MarcoB Mar 20 '21 at 20:33Normal@Series[..]to get rid of the big-O term, if you like. – Michael E2 Mar 20 '21 at 20:45