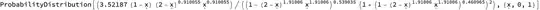1

I had defined pdf of distribution, generate data and specify the least square function.I am not aware of the code for finding estimators and bias of this distribution using method of least square estimation. I am trying to implement simulation. can anyone help me to do this.

f[\[Alpha]_, \[Lambda]_] := 
 ProbabilityDistribution[(
  4*\[Lambda]*\[Alpha]*
   x^(\[Alpha] - 1)*(1 - x)*(2 - x)^(\[Alpha] - 
    1)*(1 - x^\[Alpha]*(2 - x)^\[Alpha])^(\[Lambda] - 
    1))/(1 + (1 - x^\[Alpha]*(2 - x)^\[Alpha])^\[Lambda])^2, {x, 0, 
   1}, Assumptions -> \[Alpha] > 0 && \[Lambda] > 0]

x = RandomVariate[f[2, 0.5], 50]


The least square function  is defined by


l = !(
*UnderoverscriptBox[([Sum]), (i = 1), (n)]
*SuperscriptBox[((
*FractionBox[(1 - 
*SuperscriptBox[((1 - 
*SuperscriptBox[(x), ([Alpha])]*
*SuperscriptBox[((2 - 
              x)), ([Alpha])])), ([Lambda])]), (1 + 
*SuperscriptBox[((1 - 
*SuperscriptBox[(x), ([Alpha])]*
*SuperscriptBox[((2 - x)), ([Alpha])])), ([Lambda])])] - 
*FractionBox[(i), (n + 1)])), (2)])enter code here
Akhilraj N S
  • 115
  • 4
  • It is not clear to me what you are doing. You define a model PDF. To fit this model to some data you need data that are not calculated with the same PDF. The least square error function should then be a function of the difference between the fu8nction values calculated with your PDF and the values that are obntained independend of it. – Daniel Huber Mar 21 '21 at 09:18
  • Actually i want to do simulation. For that i defined the pdf of the distribution, generate sample from it. Then i specify the least square function. I do not know how to find estimates from this specified least square function.@DanielHuber – Akhilraj N S Mar 21 '21 at 12:20

2 Answers2

2
Clear["Global`*"]

Your ProbabilityDistribution is

f[α_, λ_] = ProbabilityDistribution[
   (4*λ*α*x^(α - 1)*(1 - x)*(2 - x)^(α - 1)*
      (1 - x^α*(2 - x)^α)^(λ - 1))/
    (1 + (1 - x^α*(2 - x)^α)^λ)^2, {x, 0, 1}, 
   Assumptions -> α > 0 && λ > 0];

The source distribution for the data is

dist = f[2, 1/2];

The Mean and StandardDeviation for this specific distribution are

{μ, σ} = Through[{Mean, StandardDeviation}[dist]] // FullSimplify

(* {3 - Sqrt[2] - ArcCoth[Sqrt[2]], 
 1/2 √(-36 + 16 Sqrt[2] + 4 π - Log[2 - Sqrt[2]]^2 + 
     Log[2 + Sqrt[2]]^2 - 4 ArcSinh[1] (-4 + 2 Sqrt[2] + Log[2 + Sqrt[2]]))} *)

with approximate numeric values of

{μ, σ} // N

(* {0.704413, 0.232854} *)

Generating sample data

SeedRandom[1234];
data = RandomVariate[dist, 50];

{m, s} = Through[{Mean, StandardDeviation}[data]]


(* {0.726298, 0.240181} *)

Using FindDistributionParameters, the maximum likelihood parameter estimates are

param = FindDistributionParameters[data, f[α, λ]]

(* {α -> 1.91006, λ -> 0.460965} *)

Alternatively, using EstimatedDistribution

distEst = EstimatedDistribution[data, f[α, λ]]

enter image description here

The results are equivalent

distEst === (f[α, λ] /. param)

(* True *)

Comparing the PDFs for the source distribution and the estimated distribution

Plot[
 {PDF[dist, x], PDF[distEst, x]},
 {x, 0, 1 - 10^-6},
 AxesLabel -> (Style[#, 14, Bold] & /@ {"x", "PDF"}),
 PlotLegends ->
  Placed[{"actual", "estimated"}, {0.5, 0.5}]]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
2

@BobHanlon provided the answer you should use if you want to have a reasonable procedure to estimate the parameters from that distribution.

But suppose you wanted to look at what happens when crazy folks want to use least squares to estimate the parameters.

The sum of squares you list (slightly modified) is

Sum of squares

So it appears that you're comparing the CDF against the cumulative probability of the sample ($i/(n+1)$). (I'm ignoring the use of $n+1$.)

To do that you need to sort the random sample from low to high. The code for the least squares estimates would then be

n = 50;
SeedRandom[12345];
y = Sort[RandomVariate[f[2, 0.5], n]]
l = Sum[((1 - (1 - y[[i]]^α*(2 - y[[i]])^α)^λ)/(1 + (1 - y[[i]]^α*(2 - y[[i]])^α)^λ) - i/(n + 1))^2,
  {i, n}];
FindMinimum[{l, α > 0, λ > 0}, {{α, 2}, {λ, 0.5}}]
(* {0.0370631, {α -> 3.43064, λ -> 0.656073}} *)
JimB
  • 41,653
  • 3
  • 48
  • 106