0

I have a second order differential equation with two known initial conditions like this:

s = NDSolve[{Y''[x] == -2 δ1/Y[x], Y'[0] == 0, Y[0] == R0i}, Y, {x, 0, 40000}, WorkingPrecision -> 10];

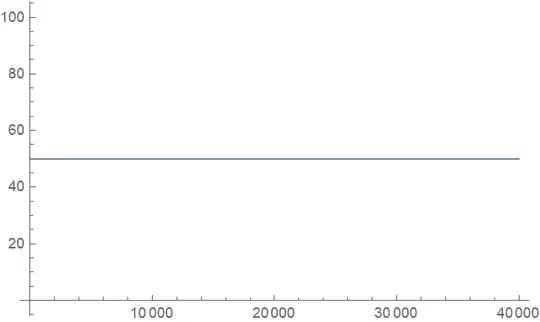
Plot[Evaluate[Y[x] /. s], {x, 0, 40000}, PlotRange -> All]

It worked:

enter image description here

Then I tried the integrate this second order differential equation with two known initial condition，integrate both sides with respect to x and you can get 1/2 (Y'[x])^2 + 2 δ1 Log[Y[x]] = a, then use two known initial conditions Y'[0] == 0, Y[0] == R0i to determine the value of a, then you get:

Y'[x] == Sqrt[4 δ1 Log[R0i/Y[x]]]

But when I try to solve this first order differential equation I got above

s = NDSolve[{Y'[x] == Sqrt[4 δ1 Log[R0i/Y[x]]], Y[0] == R0i}, Y, {x, 0, 40000}];

Plot[Evaluate[Y[x] /. s], {x, 0, 40000}, PlotRange -> All]

I get the different answer1:

enter image description here

And the different answer2 with error message:

NdSolve :: ICRES: NdSolve computation gives the initial value of zero residuals to the differential system, but some components differ from those specified. If they need to be met, it is recommended that explicit initial values be given to all dependent variables.

s = NDSolve[{Y'[x] == Sqrt[4 δ1 Log[R0i/Y[x]]], Y'[0] == 0}, 
   Y, {x, 0, 40000}];

Plot[Evaluate[Y[x] /. s], {x, 0, 40000}, PlotRange -> All]

enter image description here

Does anybody know what the problem is? Maybe it's more of a math problem.

The initial conditions are as follows:

δ = 1.213183119 10^-6;
δ1 = (1 - 1/100) δ;
R0i = 50;
shrocat
  • 189
  • 7
  • 2
    Your equation has the form eq = Y''[x] == -2 \[Delta]1/Y[x];. If you solve it DSolve[{eq, Y'[0] == 0, Y[0] == R0i}, Y, x] the solution yields Y -> Function[{x}, E^-InverseErf[-((2 x Sqrt[\[Delta]1])/(Sqrt[\[Pi]] R0i))]^2 R0i. This is not the expression Y'[x] == Sqrt[4 δ1 Log[R0i/Y[x]]] that you gave in the question. So, how did you obtain the latter expression? – Alexei Boulbitch Mar 24 '21 at 14:45
  • 2
    The initial condition Y[0] == R0i is an obvious singular point of the vector field, i.e., it makes Y'[x] equal to zero. Hence the constant solution. -- I believe you have a sign error, too. Start just below the singular point: NDSolve[{Y'[x] == Sqrt[4 \[Delta]1 Log[R0i/Y[x]]], Y[0] == R0i (1 - $MachineEpsilon)}, Y, {x, 0, 40000}]. (I wouldn't use WorkingPrecision -> 10, but if you do, you'll have to use a bigger number than $MachineEpsilon probably.) – Michael E2 Mar 24 '21 at 15:38
  • @AlexeiBoulbitch Multiply both sides of the ODE by Y'[x] and integrate with respect to x. – Michael E2 Mar 24 '21 at 15:40
  • 1
    @ OP, FWIW (I don't know how familiar you are with DEs), your 1st-order DE is like the one in the lower left graphics of Fig. 3 here. The thicker red line shows the singular solution ($y=$ constant in your case). NDSolve cannot numerically distinguish between your desired solution and the singular solution at an initial condition on the singular solution. A typical way to resolve the singularity is to differentiate the DE, which takes you back to your original 2nd-order DE – Michael E2 Mar 24 '21 at 16:13
  • Oops, I seem to have dropped the minus sign in front of the Sqrt[] that is needed to get the desired solution. Darn. Can’t edit comments. If it’s a satisfactory solution, I can make it an answer and fix it. – Michael E2 Mar 24 '21 at 18:31
  • @Alexei Boulbitch You can integrate both sides with respect to x and you can get 1/2 (Y'[x])^2 + 2 δ1 Log[Y[x]] = a, then use two known initial conditions Y'[0] == 0, Y[0] == R0i to determine the value of a, then you get Y'[x] == Sqrt[4 δ1 Log[R0i/Y[x]]] – shrocat Mar 25 '21 at 01:20
  • @Michael E2, Thanks for your reply. Well, my understanding of DEs is still in the beginner stage of higher mathematics in my undergraduate study(It's really embarrassing), and I will try to understand your answer. And Other questions about the WorkingPrecision, I use WorkingPrecision -> 50 but it still Popup error message: "The differential equation has an accuracy less than WorkingPrecision 10, but it should be bigger than $MachineEpsilon, why the error came up? – shrocat Mar 25 '21 at 01:52
  • The precision of your system is MachinePrecision. I would just omit the WorkingPrecision option until you better understand how arbitrary precision numbers work. MachinePrecision is consider to be just slightly less than 16. Setting WorkingPrecision higher than that results in a warning. It's only a warning, not an error. Mathematica assumes that if you wanted to do a computation at a certain working precision, the user would supply input at that precision or higher. – Michael E2 Mar 25 '21 at 02:13
  • @ Michael E2 Thank you for answering my confusion! – shrocat Mar 25 '21 at 05:50

0 Answers0