How to make a circular heat map or diagram in Mathematica?

Question

Is there any way to make a circular heat map in Mathematica?

Thanks for your help!

Here is a toy example for regular heat map. Can anyone help me make it to a circular one?

data1={{9., 1., 6., 7., 6., 3., 1., 3., 10., 2., 2., 5., 2., 5., 3., 
  1.}, {5., 5., 5., 4., 4., 6., 4., 6., 9., 1., 2., 10., 2., 1., 1., 
  6.}, {2., 7., 6., 2., 8., 10., 8., 9., 2., 5., 3., 9., 7., 8., 7., 
  5.}, {6., 6., 2., 1., 8., 2., 8., 3., 8., 5., 5., 4., 6., 2., 3., 
  6.}, {8., 1., 8., 2., 5., 8., 5., 3., 5., 3., 4., 2., 2., 4., 4., 
  1.}, {10., 2., 8., 10., 3., 6., 1., 9., 3., 5., 2., 5., 1., 3., 7., 
  9.}};
ArrayPlot[data1, ColorFunction -> ColorData["LightTerrain"], 
 Frame -> True, 
 FrameTicks -> {{{{1, "r1"}, {2, "r2"}, {3, "r3"}, {4, "r4"}, {5, 
      "r5"}, {6, "r6"}}, None},
   {None, {{1, "c1"}, {2, "c2"}, {3, "c3"}, {4, "c4"}, {5, "c5"}, {6, 
      "c6"}, {7, "c7"}, {8, "c8"}, {9, "c9"}, {10, "c10"}, {11, 
      "c11"}, {12, "c12"}, {13, "c13"}, {14, "c14"}, {15, "c15"}, {16,
       "c16"}}}}, 
 Epilog -> {Text["Sector1", {2, 8}], Text["Sector2", {6, 8}], 
   Text["Sector3", {10, 8}], Text["Sector4", {14, 8}]}, 
 ImagePadding -> {{20, 20}, {20, 80}}, ImageSize -> Large]

I want to make a circular diagram like the following one.

Reference: https://stackoverflow.com/questions/62556246/how-to-plot-the-variant-circular-bar-chart-in-r-with-ggplot

Is it possible to make a one like this?

Thanks a lot!

@kglr Hi kglr, is there any way to plot the dendrogram shown in the 1st circular diagram example for illustrating the seven categories? The example looks very neat. I don't know how to make a similar one in Mathematica. Thanks again for your guidance. — Frankie, Apr 01 '21 at 16:20
Hi Frankie. I was afraid that question was coming:) It can be done using a custom ChartElementFunction. I will update my answer if I come up with a clean way to do it. — kglr, Apr 01 '21 at 16:28
@kglr Hi kglr, thank you very much for your quick reply and look forward to your kind help! — Frankie, Apr 02 '21 at 15:37

kglr · Answer 1 · 2021-03-31T06:20:22.587

A more flexible approach: Pre-process input data to construct a data set for SectorChart. To inject an angular gap in the chart, we add a last column to input data and assign to it {}& as the ChartElementFunction (so that it is not rendered). The size of the gap is controlled by the second argument of the function preProcessData.

ClearAll[preProcessData, circularLegend, labelingFunction]
preProcessData[data_, gap_: Automatic, clr_: "Rainbow"] := 
  Module[{del = gap /. Automatic -> 1/16, 
   slices = ConstantArray[1/#[[2]], #] & @ Dimensions[data]}, 
  Append[del -> {Null, 0}] /@ 
    MapThread[Thread[# -> Transpose[{##2}]] &, 
     {Rescale[slices, {0, 1}, {0, 1 - del}], Rescale @ data, data}] /. 
   Rule[a_, {b1_, b2_}] :> Style[Labeled[{a, 1}, b2, Tooltip], ColorData[clr] @ b1]]
circularLegend[min_, max_, colorscheme_: "Rainbow"] := 
  AngularGauge[min, {min, max}, ScaleOrigin -> {{Pi/2, 2 Pi}, 1.1}, 
   ScaleRanges -> ({#, .3} & /@ Partition[Subdivide[min, max, 50], 2, 1]),
   "TickSide" -> Left, "LabelSide" -> Left, 
   "TickLength" -> {Scaled[.04], Scaled[0.02]}, 
   TicksStyle -> FontSize -> Scaled[.07], GaugeMarkers -> None, 
   ScaleRangeStyle -> colorscheme, GaugeFrameStyle -> None]
labelingFunction[nrows_, collabels_] := If[#2[[1]] == nrows, 
   Placed[collabels[[#2[[2]]]], {1/2, 1.1}]] &

Examples:

columnlabels = Append[Style["c" <> ToString@#, 14] & /@ 
    Range[Last@Dimensions[data1]], ""];
rowlabels = Style[2010 + #, 16] & /@ Range[First @ Dimensions @ data1];
radialorigin = 4;
gap = 1/16;
SectorChart[preProcessData[data1], 
 SectorOrigin -> {{Pi/2 + gap Pi, "Counterclockwise"}, radialorigin},
 ChartBaseStyle -> Directive[EdgeForm[{Opacity[1], White}]],
 LabelingFunction -> labelingFunction[First@Dimensions@data1, columnlabels], 
 ChartElementFunction -> Append[ConstantArray["Sector", Length@First@data1], {} &], 
 ChartLegends -> Placed[circularLegend[Min@data1, Max@data1], Center], 
 ImageSize -> 700, SectorSpacing -> {0, 0}, 
 Epilog -> {Text[Style["Legend", Black, 16], {0, 0}], 
   MapIndexed[Text[#, {0, radialorigin - 1/2 + #2[[1]]}] &, rowlabels]}]

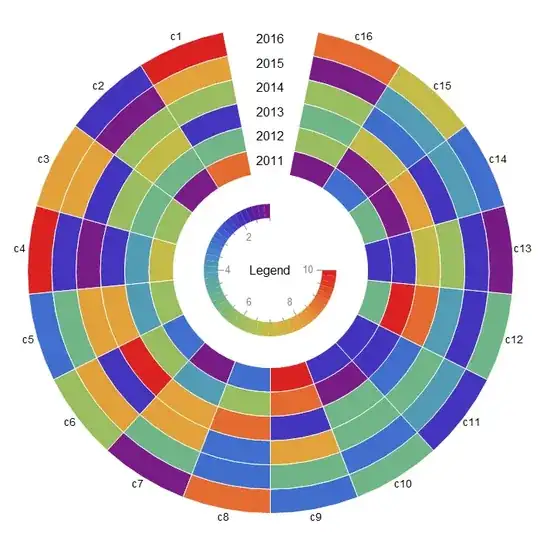
Use preProcessData[data1, gap, "LightTerrain"] and circularLegend[Min@data1, Max@data1, "LightTerrain"] to get

To have a gap in the positive quadrant, use

SectorChart[preProcessData[data1, 1/4, "LightTerrain"], 
 SectorOrigin -> {{Pi/2, "Counterclockwise"}, radialorigin},
 ChartBaseStyle -> Directive[EdgeForm[{Opacity[1], White}]],
 LabelingFunction -> labelingFunction[First@Dimensions@data1, columnlabels],
 ChartElementFunction -> Append[ConstantArray["Sector", Length@First@data1], {} &], 
 ChartLegends -> Placed[circularLegend[Min@data1, Max@data1,  "LightTerrain"],  Center],
 ImageSize -> 700, SectorSpacing -> {0, 0}, 
Epilog -> {Text[Style["Legend", Black, 16], {0, 0}], 
   MapIndexed[Text[#, Offset[{30, 0}, {0, radialorigin - 1/2 + #2[[1]]}]] &, 
    rowlabels]}]

Using other built-in ChartElementFunctions:

Multicolumn[SectorChart[preProcessData[data1, 1/4], 
    SectorOrigin -> {{Pi/2, "Counterclockwise"}, radialorigin}, 
    ChartBaseStyle -> Directive[EdgeForm[{Opacity[1], White}]], 
    LabelingFunction -> labelingFunction[First@Dimensions@data1, columnlabels], 
    ChartElementFunction -> 
     Append[ConstantArray[
       ChartElementDataFunction[#, "AngularFrequency" -> 50, 
        "RadialAmplitude" -> 0.2], Length@First@data1], {} &], 
    ImageSize -> Medium, SectorSpacing -> {0, 0}, 
    Epilog -> {Text[Style[#, 16], {0, 0}, {-1, -3}], 
      MapIndexed[Text[#, Offset[{30, 0}, {0, radialorigin - 1/2 + #2[[1]]}]] &, 
       rowlabels]}] & /@ 
   {"TriangleWaveSector", "SquareWaveSector", "OscillatingSector", "NoiseSector"}, 2]

Multiple data sets:

SeedRandom[1]
data2 = RandomReal[{25, 100}, {8, Last@Dimensions@data1}];
data3 = RandomInteger[{10, 30}, {4, Last@Dimensions@data1}];
{rowlabels1, rowlabels2, rowlabels3} = Style[2010 + #, 16] & /@ 
  Range[First@Dimensions@#] & /@ {data1, data2, data3};
radialorigin = 4;
radialorigin2 = radialorigin + 1 + First @ Dimensions @ data1;
radialorigin3 = radialorigin2 + 1 + First @ Dimensions @ data2;
radialorigins = {radialorigin,radialorigin2,radialorigin3};
colors = {"LightTerrain", "Rainbow", "SolarColors"};
charts = MapThread[
   SectorChart[preProcessData[#, 1/4, #2], 
     SectorOrigin -> {{Pi/2, "Counterclockwise"}, #3},
     ChartBaseStyle -> Directive[EdgeForm[{Opacity[1], White}]],
     LabelingFunction -> #4,
     ChartElementFunction -> Append[ConstantArray["Sector", Length@First@#], {} &], 
     ImageSize -> 1 -> 15, SectorSpacing -> {0, 0}] &,
   {{data1, data2, data3}, colors, radialorigins,
    {None, None, labelingFunction[First @ Dimensions @ data3, columnlabels]}}];
legends = MapThread[Inset[circularLegend[Min @ #, Max @ #,  #2], 
    {radialorigin + First[Dimensions @ data1]/2, #3 + 
       First[Dimensions @ #]/2}, Center, Scaled[{.12, .12}]] &, 
   {{data1, data2, data3}, colors, radialorigins}];

Combine the three charts using Show and add legends as Epilog:

Show[charts, 
 Epilog -> {legends, 
   MapThread[MapIndexed[Function[{x, y}, Text[x, Offset[{30, 0},
       {0, # - 1/2 + y[[1]]}]]], #2] &,
     {radialorigins, {rowlabels1, rowlabels2, rowlabels3}}],
   MapThread[Text[#2, Offset[{0, 20}, {#, 0}]] &,
     {radialorigins + (Dimensions[#][[1]]/2 & /@ {data1, data2, data3}), 
     Style["group " <> ToString@#, 16] & /@ Range[3]}]}, 
 PlotRange -> All]

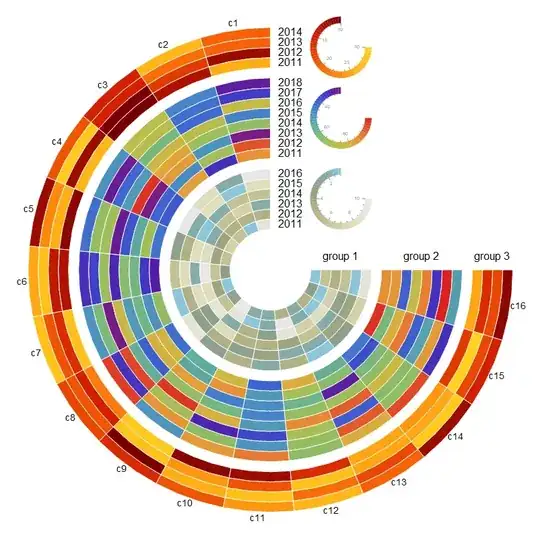
ClearAll[barLegendRow]
barLegendRow = BarLegend[{#2, #}, LegendLabel -> #3, LegendLayout -> "Row", 
    LegendMarkerSize -> {250, 30}] &;
barlegends = MapThread[barLegendRow, 
   {MinMax /@ {data1, data2, data3}, colors, 
    Style["group " <> ToString@#, 14] & /@ Range[3]}];
legends2 = MapThread[Inset[#2, 
     {radialorigin + First[Dimensions@data1]/10, #3 + 
       First[Dimensions@#]/2}, {-1, 0}, Scaled[{1, 1}]] &,
   {{data1, data2, data3}, barlegends, radialorigins}];
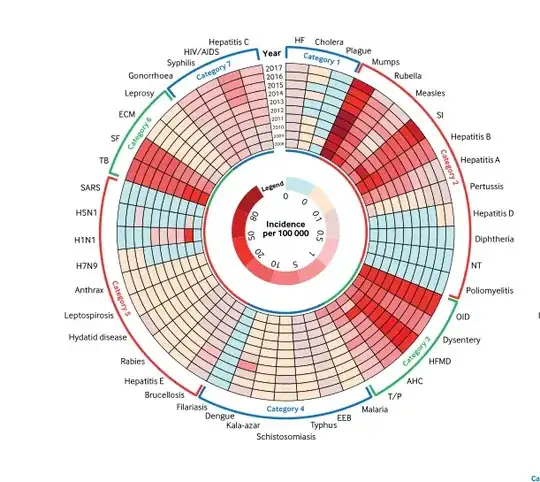
Show[charts, 
 Epilog -> {legends2, 
   MapThread[MapIndexed[Function[{x, y}, 
       Text[x, Offset[{30, 0}, {0, # - 1/2 + y[[1]]}]]], #2] &, 
     {radialorigins, {rowlabels1, rowlabels2, rowlabels3}}], 
   MapThread[Text[#2, Offset[{0, 20}, {#, 0}]] &, 
     {radialorigins + (Dimensions[#][[1]]/2 & /@ {data1, data2, data3}), 
     Style["group " <> ToString@#, 16] & /@ Range[3]}]}, 
 PlotRange -> All]

ClearAll[histogramLegend]
histogramLegend = SmoothHistogram[Flatten@#, MaxExtraBandwidths -> 0,
    PlotRange -> {MinMax @ #, Automatic}, PlotLabel -> #3, 
    ColorFunction -> Function[{x, y}, ColorData[#2][x]], 
    Filling -> Axis, Axes -> {True, False}, AspectRatio -> 1/8, 
    PlotRangePadding -> Scaled[.02], 
    PlotStyle -> LineOpacity -> 0] &;
histolegends = MapThread[histogramLegend, 
   {{data1, data2, data3}, colors, 
    Style["group " <> ToString @ #, 14] & /@ Range[3]}];
legends3 = MapThread[Inset[#2, {radialorigin + First[Dimensions@data1]/3, #3 + 
       First[Dimensions@#]/2}, Left, Scaled[{.3, .2}]] &, 
   {{data1, data2, data3}, histolegends, radialorigins}];
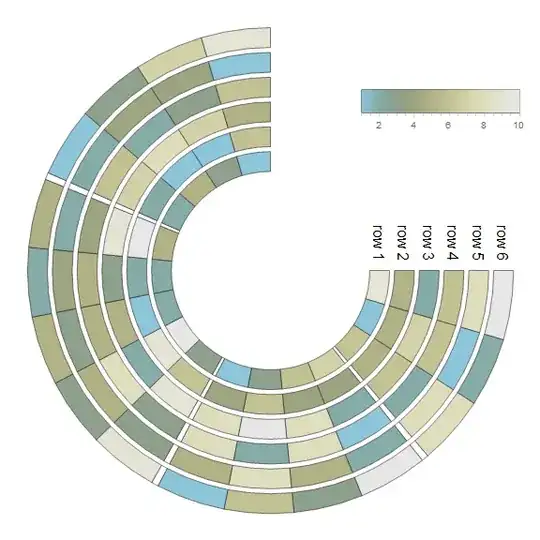
Show[charts, 
 Epilog -> {legends3, 
   MapThread[MapIndexed[Function[{x, y}, 
       Text[x, Offset[{30, 0}, {0, # - 1/2 + y[[1]]}]]], #2] &, 
    {radialorigins, {rowlabels1, rowlabels2, rowlabels3}}],
   MapThread[Text[#2, Offset[{0, 20}, {#, 0}]] &,
     {radialorigins + (Dimensions[#][[1]]/2 & /@ {data1, data2, data3}), 
     Style["group " <> ToString@#, 16] & /@ Range[3]}]}, 
 PlotRange -> All]

Impressive work! should be submitted as a ResourceFunction. — sunt05, Mar 25 '21 at 22:27
@sunt05 I agree. Many of kglr's MSE posts could become fine WFR entries. — Anton Antonov, Mar 26 '21 at 06:41
@sunt05 I agree too. Many of kglr's quick responses are far more useful than the online manual of Mathematica. I really appreciate kglr's contribution to the community! — Frankie, Mar 26 '21 at 12:07
@sunt05, anton, Frankie, thank you for the kind words. This is a great question. A ResourceFunction is a great idea. I will look into it. Given so many moving parts (input data structure with possibly many layers, layout/labeling/legending choices) it looks like a non-trivial task to put together something clean and robust . — kglr, Mar 26 '21 at 20:00
@kglr Just noticed that you are over 300K rep, congratulations! Well deserved. I really appreciate the detail and alternatives you provide in your answers. I have learned so much from them. Thank you. — Rohit Namjoshi, Mar 28 '21 at 01:42
@kglr Please add your circularLegend to the Wolfram Function Repository. It's very nice. — Edmund, Aug 17 '21 at 11:26
Leave it to the undisputed master, kglr, to craft such an elegant solution. I hope this becomes a new plot type in the next Mma release. — David G. Stork, Jan 16 '24 at 16:52

kglr · Answer 2 · 2021-03-28T20:42:15.713

For starters:

ClearAll[styledData]
styledData[data_, sectorlengths_, colorscheme_: "LightTerrain"] := 
  Fold[Function[{x, y}, Insert[#, .1 -> White, y] & /@ x], 
   Map[Tooltip[1, #] -> ColorData[colorscheme][Rescale[#, MinMax@data, {0, 1}]] &, 
    data, {-1}], 1 + Reverse @ Most @ Accumulate @ sectorlengths];
sectorlengths = {3, 4, 5, 4};
styleddata1 = styledData[data1, sectorlengths];
PieChart[MapIndexed[Labeled[#, Rotate[Style[Row[{"row ", #2[[1]]}], 16], -90 Degree], 
    {{1/2, 1/2}, {.5, -1/5}}] &, styleddata1], 
 SectorOrigin -> {Automatic, 5}, 
 ChartElementFunction -> 
   (ChartElementData["Sector"][{Rescale[#[[1]], 
      {-Pi, Pi}, {Pi/2, 2 Pi}], #[[2]]}, ##2] &),
 ChartLegends -> Placed[BarLegend[{ColorData["LightTerrain"], MinMax @ data1}, 
    LegendMarkerSize -> {30, 200}], {.8, .75}], 
 ImageSize -> Large]

Use

ChartLegends -> Placed[BarLegend[{ColorData["LightTerrain"], MinMax@data1}, 
   LegendLayout -> "Row", LegendMarkerSize -> {200, 30}], {.8, .8}]

to get

Thank you very much for your kind help and quick reply! I really appreciate your great contribution to the freshman's community! — Frankie, Mar 26 '21 at 12:10

How to make a circular heat map or diagram in Mathematica?

2 Answers2

Multiple data sets:

Linked