5

Suppose I do the following:

enter image description here

Now, If I compute:

enter image description here

Then "Mathematica stops being symbolic". Why does this happen? I want the computation to show matrix entries in terms of $a,b,c,d$, similar to the first example. Is it possible to do that?

Red Banana
  • 5,329
  • 2
  • 29
  • 47
  • 1
    Hmm, yeah, I'm not even sure how Mathematica "knows" this. After all, what if b == e == 0? You'd hope the symbolic result would hold for all values of a, b, d, e, but it seems Mathematica's making some hidden assumptions at some point. – thorimur Mar 25 '21 at 22:57
  • 1
    For that matter, why does MatrixRank[{{a, b}, {c, d}}] give 2... – thorimur Mar 25 '21 at 23:01
  • What specific different result did you expect? – Daniel Lichtblau Mar 25 '21 at 23:56
  • @DanielLichtblau It should be something like: $$\begin{pmatrix} {c}&{d}\ {0}&{\frac{bc-ad}{c}} \end{pmatrix}$$ – Red Banana Mar 26 '21 at 00:40
  • 4
    Symbolic computations in Mathematica are often generically correct, meaning that the results ignore excepts on a locus of codimension ≥ 1. Even the first result is wrong if b == 2 a. I don't really see a big difference between the two examples. – Michael E2 Mar 26 '21 at 00:56
  • That's not what RowReduce does. Which puts the question outside the scope of the forum. – Daniel Lichtblau Mar 26 '21 at 13:22
  • Surely Mathemtica ought to return a conditional result from RowReduce, etc., for such a symbolic matrix? – murray Mar 26 '21 at 14:07
  • 1
    @murray No. That's not what it is designed to do. It works over the field of rational functions in the variables present. See also this previous MSE thread (for which the present thread is essentially a duplicate). See also this. And this too might be relevant. – Daniel Lichtblau Mar 26 '21 at 14:30

2 Answers2

5

This gives the weird result in a comment that has nothing to do with the matrix {{a, b}, {d, e}} in the question:

LinearSolve[{{c, d}, {a, b}}]@"getU" // Together

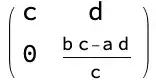
Mathematica graphics

Michael E2
  • 235,386
  • 17
  • 334
  • 747
2

Check: https://en.wikipedia.org/wiki/Gaussian_elimination

And from the documentation for RowReduce: RowReduce performs a version of Gaussian elimination, adding multiples of rows together so as to produce zero elements when possible. The final matrix is in reduced row echelon form. If m is a non-degenerate square matrix, RowReduce[m] is IdentityMatrix[Length[m]]. 

Encho Solakov
  • 91
  • 1