Efficient drawing of convex polyhedron given a set of points

Question

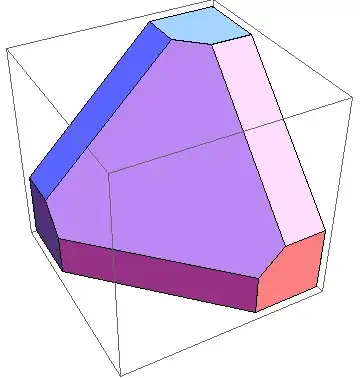
I have a set of points in the 3D space and I want to draw the bounding convex polyhedron of those points. A very naïve solution would be to draw a triangle between every three points:

Graphics3D[
    {EdgeForm[None], Polygon[Part[pts, #] & /@ Subsets[Range[Length@pts], {3}]]}, 
    Axes -> True]

However, this method is very inefficient. It takes a few seconds to be drawn on my laptop and whenever I want to rotate it using the mouse, it doesn't move smoothly. I know what the issue is: I am drawing too many triangles, many of them are not even visible (since they are placed inside the polyhedron). But how can I fix it?

Here is an example and the set of the points:

Polyhedron

pts={{0., 0., 0.}, {0., 0., 1.79176}, {0., 1.79176, 0.}, {1.79176, 0., 
  0.}, {0., 1.79176, 0.}, {0., 0., 1.79176}, {1.79176, 0., 0.}, {0., 
  1.79176, 0.606136}, {0., 0.606136, 1.79176}, {0., 1.79176, 
  0.606136}, {0., 0.606136, 1.79176}, {1.79176, 0., 
  0.606136}, {0.606136, 0., 1.79176}, {1.79176, 0.606136, 
  0.}, {0.606136, 1.79176, 0.}, {1.79176, 0., 0.606136}, {0.606136, 
  0., 1.79176}, {1.79176, 0.606136, 0.}, {0.606136, 1.79176, 
  0.}, {1.79176, 0., 0.}, {0., 1.79176, 0.}, {0., 0., 
  1.79176}, {1.79176, 0., 0.606136}, {0.606136, 0., 
  1.79176}, {1.79176, 0.606136, 0.}, {0.606136, 1.79176, 0.}, {0., 
  1.79176, 0.606136}, {0., 0.606136, 1.79176}, {0., 1.79176, 
  0.606136}, {0., 0.606136, 1.79176}, {1.79176, 0.606136, 
  0.}, {0.606136, 1.79176, 0.}, {1.79176, 0., 0.606136}, {0.606136, 
  0., 1.79176}, {1.79176, 0.606136, 0.}, {0.606136, 1.79176, 
  0.}, {1.79176, 0., 0.606136}, {0.606136, 0., 1.79176}, {1.79176, 
  0.606136, 0.}, {0.606136, 1.79176, 0.}, {1.79176, 0., 
  0.606136}, {0.606136, 0., 1.79176}, {0., 1.79176, 0.606136}, {0., 
  0.606136, 1.79176}, {0., 1.79176, 0.606136}, {0., 0.606136, 
  1.79176}, {1.79176, 0.606136, 0.374693}, {1.79176, 0.374693, 
  0.606136}, {0.606136, 1.79176, 0.374693}, {0.374693, 1.79176, 
  0.606136}, {0.606136, 0.374693, 1.79176}, {0.374693, 0.606136, 
  1.79176}, {1.79176, 0.606136, 0.374693}, {1.79176, 0.374693, 
  0.606136}, {0.606136, 1.79176, 0.374693}, {0.374693, 1.79176, 
  0.606136}, {0.606136, 0.374693, 1.79176}, {0.374693, 0.606136, 
  1.79176}, {1.79176, 0.606136, 0.374693}, {1.79176, 0.374693, 
  0.606136}, {0.606136, 1.79176, 0.374693}, {0.374693, 1.79176, 
  0.606136}, {0.606136, 0.374693, 1.79176}, {0.374693, 0.606136, 
  1.79176}, {1.79176, 0.606136, 0.374693}, {1.79176, 0.374693, 
  0.606136}, {0.606136, 1.79176, 0.374693}, {0.374693, 1.79176, 
  0.606136}, {0.606136, 0.374693, 1.79176}, {0.374693, 0.606136, 
  1.79176}, {1.79176, 0.606136, 0.374693}, {1.79176, 0.374693, 
  0.606136}, {0.606136, 1.79176, 0.374693}, {0.374693, 1.79176, 
  0.606136}, {0.606136, 0.374693, 1.79176}, {0.374693, 0.606136, 
  1.79176}, {1.79176, 0.606136, 0.374693}, {1.79176, 0.374693, 
  0.606136}, {0.606136, 1.79176, 0.374693}, {0.374693, 1.79176, 
  0.606136}, {0.606136, 0.374693, 1.79176}, {0.374693, 0.606136, 
  1.79176}}

score 7 · Accepted Answer · 2013-04-29T07:33:07.547

7

The documented (!) TetGenConvexHull can compute the convex hull. Then using a GraphicsComplex will be efficient:

<< TetGenLink`
{coords, incidences} = TetGenConvexHull[pts];
Graphics3D[{EdgeForm[], GraphicsComplex[coords, Polygon[incidences]]}]

enter image description here

edited Apr 29 '13 at 07:33

answered Apr 29 '13 at 07:12

This should certainly be preferred... :) – J. M.'s missing motivation Apr 29 '13 at 07:36
@J.M., I just could not resist. :-) – Apr 29 '13 at 07:55
1

@ruebenko Is there an easy way to keep only "real" edges and discard the facets triangulations? (not sure if my question is clear enough ... to see what I mean just don't use EdgeForm[] in your code) – Dr. belisarius Apr 29 '13 at 11:35
To rephrase @bel's query: how does one merge polygons in the output of TetGenConvexHull[] if they are supposedly coplanar? – J. M.'s missing motivation Apr 29 '13 at 11:38
@J.M. Yours is a stronger (and preferable) request. I only asked about how to "hide" undesired edges. – Dr. belisarius Apr 29 '13 at 11:42
Not directly possible. You'd have to compute the surface triangle normals, then check if the neighbouring facets have a close enough normal and select according to some criterion. Consider: SphericalNonUniformDistribution[num_] := Table[{Cos[#1] Sin[#2], Sin[#1] Sin[#2], Cos[#2]} &[ Random[Real, {0, 2 Pi}], Random[Real, {0, Pi}]], {num}] – Apr 29 '13 at 12:00
I suppose a criterion like Norm[Cross[normal1, normal2]] <= tol might work, then... – J. M.'s missing motivation Apr 29 '13 at 12:10
Yes, that's a good choice. – Apr 29 '13 at 12:51

J. M.'s missing motivation · Answer 2 · 2013-04-29T06:57:43.910

6

The (undocumented!) function ComputationalGeometry`Methods`ConvexHull3D[] is up to the task for this particular case:

ComputationalGeometry`Methods`ConvexHull3D[pts, Axes -> None,
                                           Graphics`Mesh`FlatFaces -> False]

some convex polyhedron

edited Apr 29 '13 at 06:57

answered Apr 29 '13 at 06:46

J. M.'s missing motivation

124,525
11
401
574

I found Graphics`Mesh`FlatFaces failing (i.e. not terminating) with larger point sets in the past. Like here http://mathematica.stackexchange.com/a/23024/193 – Dr. belisarius Apr 29 '13 at 11:52
@bel, yeah, I've encountered that too during the construction of one of my former avatars. I don't know any workaround either. :( – J. M.'s missing motivation Apr 29 '13 at 11:53

Efficient drawing of convex polyhedron given a set of points

2 Answers2