1

The original function is:x^2-4x+7cos(x) I attempted to find concavity on the interval [-4,4]using mathematica but i'm not quite there yet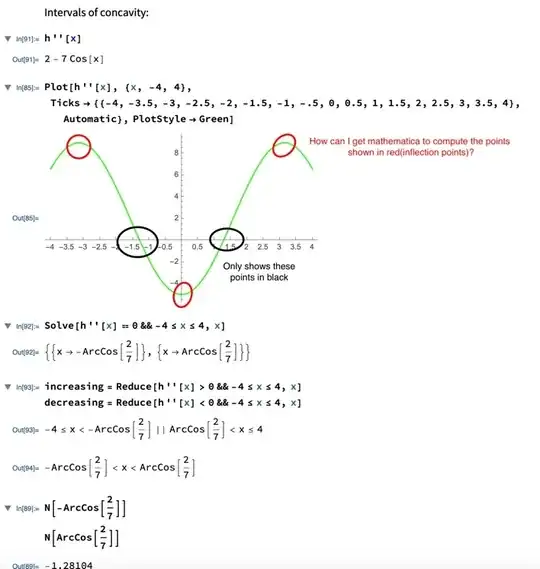enter image description here

Allan Rogers
  • 75
  • 4
  • 1
    The points in red are not actually inflection points! The concavity of h only changes at the x-values marked in black. Test: curve your hand like a C and hold your arm in front of you so that your forearm is parallel to the x-axis. Can you adjust your hand so that it fits the curve h? If so, it's concave-down. (Which hand you use doesn't matter.) – thorimur Mar 31 '21 at 00:03
  • oh I see thank you! I just assumed that when the graph changes the shape of its curve like shown it indicates a change in concavity – Allan Rogers Mar 31 '21 at 00:08
  • so the inflection points are -arccos(2/7) and arccos(2/7)? – Allan Rogers Mar 31 '21 at 00:16
  • 1
    yup! that's right. (Note the change in sign that we see here is important.) – thorimur Mar 31 '21 at 00:21

1 Answers1

2

An automatic approach is as follows.

FunctionConvexity[{x^2 - 4 x + 7*Cos[x], RealAbs[x] <= 4}, x]

Indeterminate

This means that the funciton under consideration is neither convex nor concave on the interval x >= -4, x <= 4. See the documentation for more info.

user64494
  • 26,149
  • 4
  • 27
  • 56
  • Moreover, FunctionConvexity[{x^2 - a*x + 7*Cos[x], RealAbs[x] <= 4}, x, GenerateConditions -> True] results in ConditionalExpression[ Indeterminate, Element[a, Reals]]. This means the function is neither convex nor concave on x>=-4,x<=4 for each real value of a – user64494 Mar 31 '21 at 04:27