Laplacian and NDSolve and DSolve

Question

I am trying to solve a simple test example using Laplacian. But I step from one problem to the next.

First I did not realized, that MMA uses spherical coordinates in the order: r,theta,phi and not, as I was accustomed to: r,phi,theta. Now as this is corrected, I get a constant instead of the expected function:

Consider a unit sphere having an electrostatic potential of 1. It is well know that the potential in the 3D charge free outside this sphere is 1/r.

Using Laplacian in spherical coordinates, this can be written by:

Clear[sol, f, r, ph, th]
rmax = 10;
sol[r_, th_, ph_] = 
 f[r, th, ph] /. 
  NDSolve[{Laplacian[f[r, th, ph], {r, th, ph}, "Spherical"] == 0, 
     f[1, th, ph] == 1}, 
    f, {r, 1, rmax}, {th, 0, Pi}, {ph, -Pi, Pi}][[1]]
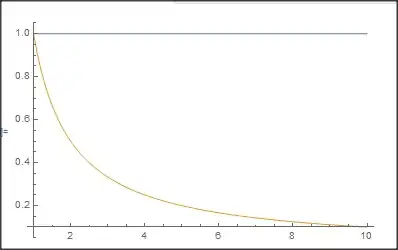
Plot[{sol[r, 0, 0], 1/r}, {r, 1, rmax}, PlotRange -> All]

Instead of 1/r I get a constant of 1, independent of rmax.

Further, if I give a periodic boundary condition., MMA complains about an "overdetermined system". And MMA can not do the calculation with increased working precision.

DSolve does not even give a result, it simply gives the equation back.

Update:

As xzczd remarked, if no boundary condition at infinity is given, MMA assumes Neumann conditions, that is it sets the derivatives to zero, what then gives a constant for the solution.

Therefore I choose rmax =100 (large enough) and specify `` f[rmax, th, ph] == 0`:

Clear[sol, f, r, ph, th]
rmax = 100;
sol[r_, th_, ph_] = 
 f[r, th, ph] /. 
  NDSolve[{Laplacian[f[r, th, ph], {r, th, ph}, "Spherical"] == 0, 
     f[1, th, ph] == 1, f[rmax, th, ph] == 0}, 
    f, {r, 1, rmax}, {th, 0, Pi}, {ph, -Pi, Pi}][[1]]
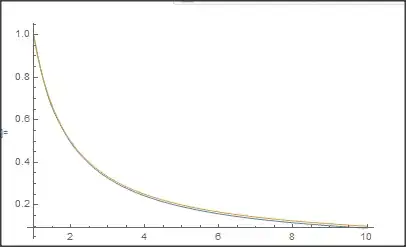
Plot[{sol[r, 0, 0], 1/r}, {r, 1, 10}, PlotRange -> All]

Now we at least get something similar to 1/r.

Uff.., earning is hard, but it is better to look like a fool for a short time than being one for the rest of ones life.