Plotting two surfaces and visualizing their intersection

Question

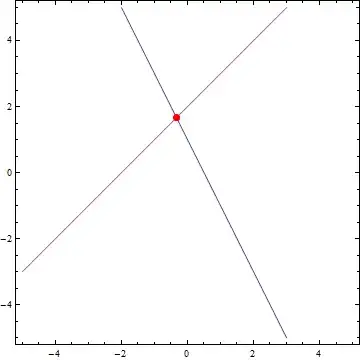
Trying to plot the following two functions to show points of intersection.

2 x + y - 1 == 0, 
x - y + 2 == 0
ContourPlot[{2 x + y - 1 == 0, x - y + 2 == 0}, {x, -5, 5}, {y, -5, 5}]

The above shows the plots, but I find it difficult to see the point of intersection. I suspect that there is a better method than this.

Please suggest a good method to plot such equations.

The intersection is the point where both lines meet. What difficulties do you have to see it? — Dr. belisarius, May 01 '13 at 01:43
True. I am unable to highlight the point and show its co-ordinates. I have looked at an approach in the following question. Is there a similar method that can be used here ? http://mathematica.stackexchange.com/questions/10472/marking-points-of-intersection-between-two-curves. — user7210, May 01 '13 at 01:53

score 4 · Answer 1 · answered May 01 '13 at 02:00

If you want to know the value of the points then you can use Solve. If you want to be able to see the intersection point highlighted then you can add a point at that value of x and y:

eqs = {2 x + y - 1 == 0, x - y + 2 == 0}
sol = {x, y} /. Solve[eqs, {x, y}]
Show[ListPlot[sol, PlotStyle -> PointSize -> 0.02],ContourPlot[Evaluate[eqs], {x, -5, 5}, {y, -5, 5}]]

score 1 · Answer 2 · answered Jan 03 '18 at 09:45

1

ContourPlot[{2 x + y - 1 == 0, x - y + 2 == 0}, {x, -5, 5}, {y, -5,  5}, 
 MeshFunctions -> {Function[{x, y}, 2 x + y - 1 - (x - y + 2)]}, 
 MeshStyle -> Directive[PointSize[Large], Red], Mesh -> {{0}}]

answered Jan 03 '18 at 09:45

kglr

394,356
18
477
896

score 0 · Answer 3 · answered Jan 03 '18 at 11:30

You could put these linear equations in matrix form:

i = LinearSolve[a = {{2, 1}, {1, -1}}, b = {1, -2}]
ContourPlot[Evaluate@Thread[a.{x, y} == b], {x, -3, 3}, {y, -3, 3}, 
 Epilog -> {Red, PointSize[0.02], Point[i]}, 
 PlotLegends -> "Expressions"]

Plotting two surfaces and visualizing their intersection

3 Answers3