2

I want to solve the following differential equation

f''[z] + (1/z)*f'[z] - f[z] + f[z]^3 == 0

subject to the boundary conditions

$$f^{\prime}(0)=0\qquad\lim_{z\to\infty}f(z)=0$$ The solution for R subject to these boundary conditions is known as Townes soliton. I have followed what is shown in the example solved here: https://mathematica.stackexchange.com/a/156362/73726.

What I have tried so far is the following:

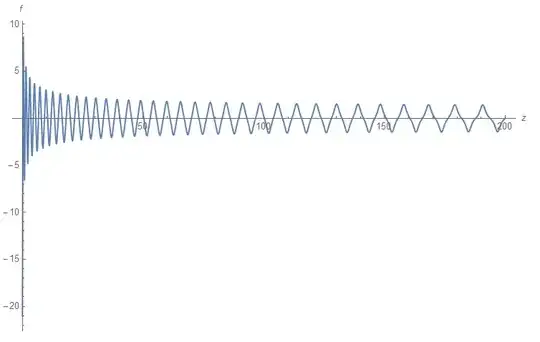
sol = NDSolveValue[{f''[z] + (1/z)*f'[z] - f[z] + f[z]^3 == 0, f[5] == 0, f'[0] == 0}, f, {z, 0, 5}, Method -> { "Shooting", "StartingInitialConditions" ->{f[5] == 100, f'[0] == 0}}];Plot[sol[z], {z, 0, 5}, AxesLabel -> {z, f}]

But it is retuning the following errors

NDSolve`Shooting::ndcinit: Initial conditions should be specified at a single point.

NDSolveValue::dsvar: 0.00010214285714285715` cannot be used as a variable.

General::stop: Further output of NDSolveValue::dsvar will be suppressed during this calculation.

HeitorGalacian
  • 95
  • 5

1 Answers1

1

Maybe this helps:

 $Version
 (*"12.2.0 for Microsoft Windows (64-bit) (December 12, 2020)"*)

sol = With[{e = 10^-30}, 
 NDSolveValue[{f''[z] + (1/z)*f'[z] - f[z] + f[z]^3 == 0, 
 f[200] == 0, f'[e] == 0}, f, {z, e, 200}, 
 Method -> {"Shooting", 
 "StartingInitialConditions" -> {f[e] == -21, f'[e] == 0}}, 
 MaxSteps -> 10^6, WorkingPrecision -> 25]]; Plot[
 sol[z], {z, 0, 200}, AxesLabel -> {z, f}, PlotRange -> All]

enter image description here

Mariusz Iwaniuk
  • 13,841
  • 1
  • 25
  • 41
  • The command of Maple 2021 evalf(dsolve({diff(f(z), z, z) + diff(f(z), z)/z - f(z) + f(z)^3 = 0, f(0) = 1/3, D(f)(0) = 0}, f(z), series, order = 20)) produces $f(z)= 0.3333333333+ 0.07407407407 z^{2}+ 0.003086419753 z^{4}- 0.00009525986892 z^{6}- 0.00001448743840 z^{8}- 5.587696941\times10^{-7} z^{10}+ 1.259010856\times10^{-8} z^{12}+ 2.608548074\times10^{-9} z^{14}+ 1.185138978\times10^{-10} z^{16}- 1.313655828\times10^{-12} z^{18}+\mathrm{O}(z^{20}) $. Since the coefficients rapidly decrease, it looks similar to a trunskated power expansion of a certain entire function. – user64494 Apr 10 '21 at 12:32