Evaluating Polynomials at Grid Points

Question

I am continuing my quest on B-splines. The code below builds a 5x5 matrix out of B-splines, using the BSplineBasis[] routine.

I now want to evaluate the polynomials that are stored in each matrix element. The problem that I am facing is, however, that each matrix element corresponds to a different position on my xy-grid.

For instance, B[[2,2]] corresponds to the grid-pint x=-1, y = -1 . B[[2,3]] corresponds to x=-1, y = 0 and so forth.

At the moment I do x = smth and then evaluate the polynomial manually. This works for a small system, but it is not optimal for larger problems.

So my question is, is there some notation that does something like B[[2,3]](put out the value of this matrix element at (x = smth,y = smth))? I tried it with Evaluate[], but didn't get it to work.

knots = {-1, -1, -1 , -1, 0, 1, 1, 1, 1};
B1 = Table[
   D[BSplineBasis[{3, knots}, i, x], {x, 2}] BSplineBasis[{3, knots}, 
     j, y], {i, 0, 4}, {j, 0, 4}];
B2 = Table[
   BSplineBasis[{3, knots}, i, x] D[
     BSplineBasis[{3, knots}, j, y], {y, 2}], {i, 0, 4}, {j, 0, 4}];
B = B1 + B2;
(*set boundary conditions*)
B[[1]] = {0, 0, 0, 0, 0};
B[[5]] = {0, 0, 0, 0, 0};
B[[All, 5]] = {0, 0, 0, 0, 0};
B[[2, 1]] = BSplineBasis[{3, knots}, 2, x];
B[[3, 1]] = BSplineBasis[{3, knots}, 3, x];
B[[4, 1]] = BSplineBasis[{3, knots}, 4, x];

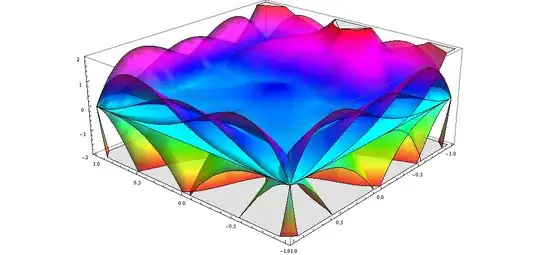
Here is a plot of what I'm doing, just for nurturing the eye.

Plot3D[Evaluate[B], {x, -1, 1}, {y, -1, 1}, Mesh -> None, 
 PlotStyle -> Directive[Opacity[0.8]], PlotRange -> {-2, 2}, 
 ColorFunction -> Function[{x, y, z}, Hue[z]]]

Answer 1

You can perform a replace:

B[[2,3]]/.{x->-1,y->0}

If you have a table of x and y values (call it xyvals) for given matrix elements then you could do:

Table[B[[m,n]]/.{x->xyvals[[m,n,1]],y->xyvals[[m,n,2]]},{m,Length[B]},{n,Length[B[[1]]]}]

Answer 2

One approach is to turn your expression into functions. I give a few extra variations just to show what can be done and which you might find useful to learn.

Here's the whole thing as a function (to be used, for example, in your Plot3D):

Bfn = Evaluate[B /. {x -> #1, y -> #2}] &;

Bfn[x, y] == B
  (* True *)

Component functions can be extracted from Bfn,

BPartFn[i_, j_] := Evaluate@Bfn[[1, i, j]] &

or from B,

BPartFn[i_, j_] := Evaluate[B[[i, j]] /. {x -> #1, y -> #2}] &

Comparisons:

BPartFn[2, 3][x, y] == B[[2, 3]]
  (* True *)

BPartFn[2, 3][-1, 0]
  (* -9/2 *)

B[[2, 3]] /. {x -> -1, y -> 0}
  (* -9/2 *)

---

If you need to evaluate them at many points, you might wish to make each function Listable:

BPartFn[i_, j_] := Function[Null, Evaluate@Bfn[[1, i, j]], Listable]

Then the function will automatically thread over lists of coordinates with a call of the form

BPartFn[2, 3][ {x1, x2, ...}, {y1, y2, ...} ]

Here are 10 points:

xy = RandomReal[{0, 1}, {10, 2}]
  (* {{0.0214747, 0.362779}, {0.00453566, 0.0420441}, {0.126681, 0.467454},
      {0.422858, 0.155077}, {0.482303, 0.920426}, {0.422345, 0.70505}, {0.572743, 0.121306},
      {0.912936, 0.601003}, {0.39634, 0.437055}, {0.542907, 0.867795}} *)

Comparison of outputs:

BPartFn[2, 3] @@ Transpose[xy]
  (* {0.321359, 0.0651208, 0.326909, 0.305393, 0.0944842, 0.150124, 
      0.263136, 0.0229906, 0.248124, 0.0690792} *)

B[[2, 3]] /. (Thread[{x, y} -> #] & /@ xy)
  (* {0.321359, 0.0651208, 0.326909, 0.305393, 0.0944842, 0.150124, 
      0.263136, 0.0229906, 0.248124, 0.0690792} *)

---

If you're going to be making a lot of calls to BPartFn, you can get a little improvement in performance by memoizing:

    BPartFn[i_, j_] := BPartFn[i_, j_] = Evaluate@Bfn[[1, i, j]] &

(It can be done with the other definitions as well.)