0

I have been examining https://library.wolfram.com/infocenter/Books/8509/DifferentialEquationSolvingWithDSolve.pdf but cannot resolve my syntax issue

eqn = 0.1*y''[x] + 2 y'[x] + 2 y[x] == 0;
sol = DSolve[{eqn, y[0] == 0, y[1] == 1}, y[x], x]

but this yields

enter image description here

I am not sure why it is written "True, True" instead of applying the boundary condition.

Haumine
  • 1
  • 2
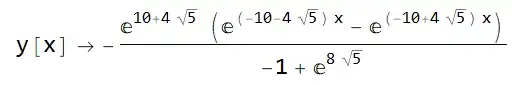
    try with clean kernel and it will work. You must have typed y[1]=1 earlier but did not show that. This explains why you got True. Also, it is Plot and not plot – Nasser Apr 16 '21 at 23:18
  • 2
    Always pay attention to the color of symbol. Your y is black, while it should be blue if it's empty. BTW, sometimes it's Derivative that's polluted: https://mathematica.stackexchange.com/q/40314/1871 https://mathematica.stackexchange.com/a/46239/1871 – xzczd Apr 17 '21 at 02:46

1 Answers1

1

This:

eqn = 0.1*y''[x] + 2 y'[x] + 2 y[x] == 0;
sol = DSolve[{eqn, y[0] == 0, y[1] == 1}, y[x], x][[1, 1]]
Plot[y[x] /. sol, {x, -5, 5}]

works returning

(*  y[x] -> 2.87407 E^(-20. x) (-1. E^(1.05573 x) + 1. E^(18.9443 x))  *)

and the following plot:

enter image description here

However, I recommend you to use the integer numbers everywhere, where it is possible. For example, using y''[x]/10 instead of 0.1*y''[x] you get this:

eqn = y''[x]/10 + 2 y'[x] + 2 y[x] == 0;
sol = DSolve[{eqn, y[0] == 0, y[1] == 1}, y[x], x][[1, 1]]

enter image description here

It is the same but looks much better. Besides, with the integer numbers, the result comes faster. The plot is, of course, the same as I displayed above.

Have fun!

Alexei Boulbitch
  • 39,397
  • 2
  • 47
  • 96