1

I have a function f[x] obtained by solving certain ODE. Thus, it is given as an interpolation function. I need to plot $\frac{dx}{df}$ as a function of $f$.

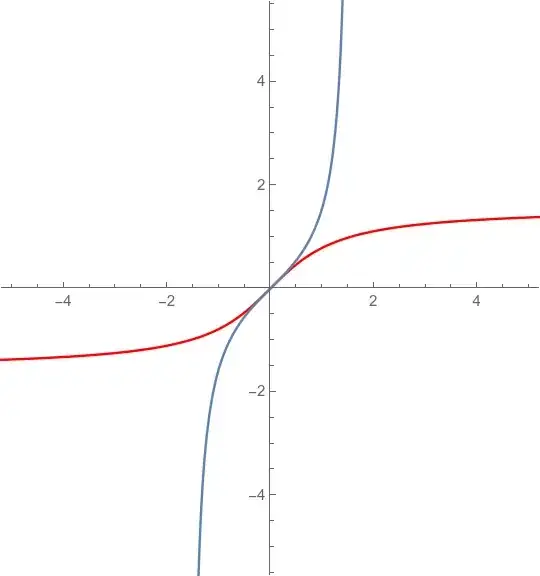
Below I will give a simple analytical example just to explain what I mean. Let $$f(x)=\arctan(x).$$ Then we have $$\frac{df}{dx}=\frac{1}{1+x^2},\quad \text{or} \quad \frac{dx}{df}=1+x^2.$$

Now we express $x$ in terms of $f$, i.e., $$x=\tan(f),$$ and substitute in the equation above: $$\frac{dx}{df}=1+x^2=1+\tan(f)^2.$$

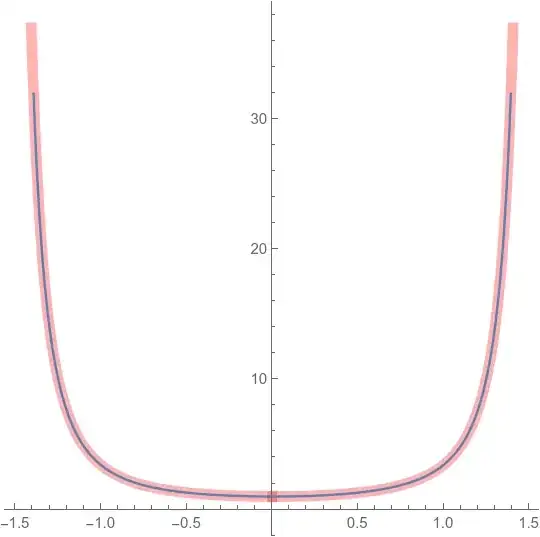
Thus, given $f(x)=\arctan(x)$, I would like to get a plot of $$1+\tan(f)^2.$$

One naive way to do it is to parametrize $f$ and $\frac{dx}{df}$ in terms of $x$ and use ParametricPlot

ParametricPlot[{f[x], 1/f'[x]}, {x, -10, 10}, AspectRatio -> 1]

However, for my numerically defined function this does not work very well. Additionally, I would like to get the dependence in a functional form, the best would be again an interpolation function. How can I achieve this, maybe it is possible to formulate the problem as ODE and use NDSolve?

yarchik
  • 18,202
  • 2
  • 28
  • 66
  • Can you simply define the inverse function fi = InverseFunction[f] and then plot fi'(y)? – Roman Apr 17 '21 at 20:43
  • @Roman I tried that too, it is much slower than ParametricPlot and suffers from similar numerical issues. – yarchik Apr 17 '21 at 20:45
  • 1
    How about adding another ODE to your solver that describes $x(f)$ so that you directly get an interpolating function for $x(f)$ from ODE solving, together with $f(x)$? – Roman Apr 17 '21 at 20:49
  • @Roman This is a good idea. In other words you are suggesting to solve $dx(f)/df=1/(df/dx)$ as a preparatory step. I have to think about it... – yarchik Apr 17 '21 at 20:53
  • For NDSolve, the dependent variables have to be functions of the same independent variable. So you cannot solve for both f(x) and x(f) at the same time as @Roman suggested. – Michael E2 Apr 18 '21 at 12:46
  • @MichaelE2 One can do something like DSolve[{y'[x] == 1/f'[y[x]], y[0] == 0}, y[x], x] in order to get the inverse of f. – yarchik Apr 18 '21 at 13:22
  • Yes but you don’t solve for f[y] at the same time. You have to solve separately, not “together.” – Michael E2 Apr 18 '21 at 13:24
  • @MichaelE2 Right, I understand what you mean. – yarchik Apr 18 '21 at 13:50
  • Related: (172677), (225880) -- One would have been a duplicate, except no-code, no-answer, so I voted to close it instead. – Michael E2 Apr 18 '21 at 14:23

2 Answers2

3

Just the same idea in How to roll a graph on the y-axis Edition 2.

Assume that the inverse function of f is g ,then f and g satisfy the equation f'[g[y]]*g'[y]==1

h[x_] := 1/(1 + x^2);
sol1 = NDSolve[{f'[x] == h[x], f[1] == π/4}, {f}, {x, -10, 10}];
sol2 = NDSolve[{h[g[y]]*g'[y] == 1, g[π/4] == 1}, {g}, {y, -1.57, 
    1.57}];
Show[Plot[{f[x] /. First@sol1}, {x, -10, 10}, PlotStyle -> Red, 
  AspectRatio -> Automatic], 
 Plot[g[y] /. First@sol2, {y, -1.57, 1.57}], PlotRange -> 5]

(* compare the result and the original post. *)


ff[x_] := ArcTan[x];
ParametricPlot[{ff[x], 1/ff'[x]}, {x, -6, 6}, AspectRatio -> 1, 
  PlotStyle -> {Opacity[.3], Red, Thickness[.02]}];
Plot[{g'[y] /. First[sol2]}, {y, -1.57, 1.57}, AspectRatio -> 1]
Show[%%, %]

enter image description here

enter image description here

cvgmt
  • 72,231
  • 4
  • 75
  • 133
3

You can more or less directly invert the interpolation table. (I may have given this answer before, but I cannot find it.) You can improve accuracy by specifying derivative values, if you have them. One needs strict monotonicity (f'[x] is nonzero and does not change sign).

Example: NDSolve by default returns an order-3 interpolation.

ode = {y'[x] == Cos[x]^2 + y[x] Sin[y[x]]^2, y[0] == 0};

ff = NDSolveValue[ode, y, {x, 0, 10}];

Order-3 inverse:

With[{
  x = Flatten@ff@"Grid",
  y = ff["ValuesOnGrid"],
  dy = ff'["ValuesOnGrid"]
  },
 iff = Interpolation[Transpose@{List /@ y, x, 1/dy}]
 ]

(* error *)
ParametricPlot[{{ff[x], iff@ff[x] - x // RealExponent}}, {x, 0, 10}, 
 PlotPoints -> 100]

Order-5 inverse: The second derivative of ff is a continuous, piecewise-linear interpolation. Using the second derivative values improves the accuracy slightly.

With[{
  x = Flatten@ff@"Grid",
  y = ff["ValuesOnGrid"],
  dy = ff'["ValuesOnGrid"],
  ddy = ff''["ValuesOnGrid"]
  },
 iff = Interpolation[Transpose@{List /@ y, x, 1/dy, -ddy/dy^3}]
 ]

ParametricPlot[{{ff[x], iff@ff[x] - x // RealExponent}}, 
 {x, 0, 10}, PlotPoints -> 100]

If you add InterpolationOrder -> All to NDSolve, the accuracy improves slightly for order 5 and above, because the higher-order derivatives are more accurate in both ff and iff. The gain is minimal and diminishes as the order increases, however.

Michael E2
  • 235,386
  • 17
  • 334
  • 747