Converting a Non-Simple Closed Curve in an Image to a Parametric Equation

Question

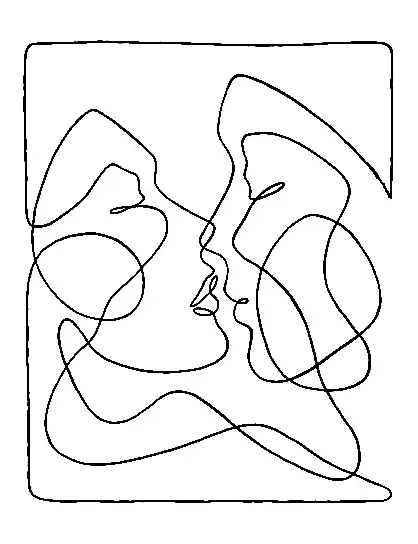
I would like to generate a parametric equation for a non-simple closed curve defined in a 2D image (shown below). This is the same problem as described in this question for simple curves.

However, when I use the solution given as an answer to this question, the resulting parametric look like the image below. I want the parametric to trace the lines, not to trace around the lines. How can I do this?

My current Mathematica code looks like this:

param[x_, m_, t_] := Module[{f, n = Length[x], nf},
  f = Chop[Fourier[x]][[;; Ceiling[Length[x]/2]]];
  nf = Length[f];
  Total[Rationalize[
     2 Abs[f]/Sqrt[n] Sin[Pi/2 - Arg[f] + 2. Pi Range[0, nf - 1] t], .01][[;; Min[m, nf]]]]]
tocurve[Line[data_], m_, t_] := param[#, m, t] & /@ Transpose[data]
dat = ImageValuePositions[
   SelectComponents[EdgeDetect@ColorNegate@Binarize@IMAGE,
    Large], 1];
ParametricPlot[
 Evaluate[tocurve[#, 500, t] & /@ {Line[
     dat[[Last[FindShortestTour[dat]]]]]}], {t, 0, 1}, Frame -> True, 
 Axes -> False]
tocurve[#, 500, t] & /@ {Line[dat[[Last[FindShortestTour[dat]]]]]}

Answer 1

img = ColorNegate[Import["https://i.stack.imgur.com/7WoZb.jpg"]];
pos = PixelValuePositions[Thinning[img], 1];

tour = Last[FindShortestTour[pos]];

(* smooth it out a bit *)
smooth = MovingAverage[pos[[tour]], 3];

intp = Interpolation[Transpose[{Subdivide[Length[smooth] - 1], smooth}]];
ParametricPlot[intp[t], {t, 0, 1}]