I'm struggling a little bit trying to understand how to address this problem, I would like to do this in mathematica: 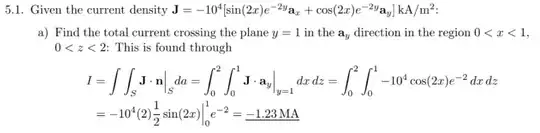 is just that I don't know how to do the dot product between $\mathbf{J}$ and $\mathbf{a}_y$ because I don't know how to define the unit vector $\mathbf{a}_y$, is it possible to do this in mathematica? thanks in advance!
is just that I don't know how to do the dot product between $\mathbf{J}$ and $\mathbf{a}_y$ because I don't know how to define the unit vector $\mathbf{a}_y$, is it possible to do this in mathematica? thanks in advance!
Asked
Active
Viewed 603 times
1
xzczd
- 65,995
- 9
- 163
- 468
diegosanchez
- 13
- 2
1 Answers
1
As shown by LouisB in the comment, use coordinate vector is the standard way to go, nevertheless, it's possible to implement the symbolic coordinate bases as follows:
Clear[Subscript]
Subscript /: Subscript[a, x_]^2 = 1;
Subscript /: Subscript[a, x_] Subscript[a, y_] /; x =!= y = 0;
Subscript[a_, b : x | y | z] := Subscript[a, ToString@b]
J = -10^4 (Subscript[a, x] Sin[2 x] E^(-2 y) + Subscript[a, y] Cos[2 x] E^(-2 y)) 10^3
Integrate[J Subscript[a, y] /. y -> 1, {z, 0, 2}, {x, 0, 1}] // N
Or more rigorously:
Clear[Subscript]
Subscript /: Subscript[a, x_].Subscript[a, x_] = 1;
Subscript /: Subscript[a, x_].Subscript[a, y_] = 0;
Subscript[a_, b : x | y | z] := Subscript[a, ToString@b]
J = -10^4 (Subscript[a, x] Sin[2 x] E^(-2 y) + Subscript[a, y] Cos[2 x] E^(-2 y)) 10^3
Integrate[J.Subscript[a, y] /. y -> 1 // TensorExpand, {z, 0, 2}, {x, 0, 1}] // N
xzczd
- 65,995
- 9
- 163
- 468
-
Thank you very much for your help @xzczd, in your code there are some things I still don't understand because I'm new using Mathematica but I will research and try to learn more, thank you for helping me out! – diegosanchez May 10 '21 at 22:50
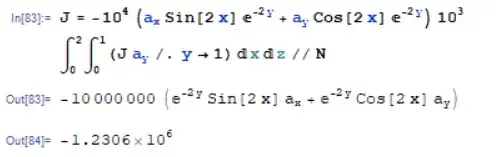
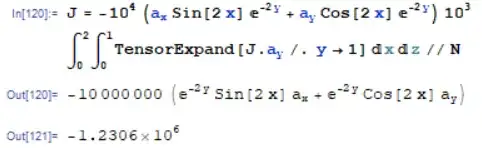
UnitVector[1]andUnitVector[2]? OrUnitVector[3, 1]etc. – Michael E2 May 10 '21 at 04:43ax = {1, 0, 0}; ay = {0, 1, 0};j = -10^4 Exp[-2 y] (Sin[2 x] ax + Cos[2 x] ay);Integrate[j.ay /. y -> 1, {z, 0, 2}, {x, 0, 1}] // N– LouisB May 10 '21 at 05:50