How to solve this integro-dfferential equation

Question

I am trying to solve a complicated system of integro-differential equations, but a MWE of my problem is the following:

fun[rho_?NumericQ, r_?NumericQ] := r NIntegrate[rho r1^2, {r1, 0, r}];
NDSolve[{R'[r] == D[fun[R[r], r], r], R[0] == 1}, R, {r, 0, 1}]

The code runs forever without producing any output: how can I solve this kind of equations?

EDIT a solution for this equation is to derive once more in $r$ and substitute back R'[r], but my system is much more complicated and I do not know the initial values for the derivatives.

EDIT2 I have tried the following code:

NDSolve[{R'[r]==D[r NIntegrate[r1^2 R[r1],{r1,0,r}],r],R[0]==1},R,{r,0,1}]

but Mathematica complaints that r us not a valid number for an extreme of integration.

How can I solve theis problem?

Answer 1

TL;DR I'm not sure if either of my attempts are correct, will update later.

Attempt 1:

First SE post I've written so I apologize in advance if anything is out of order. The error messages from the OP coming from NIntegrate could be because NIntegrate usually has a hard time dealing with symbolic limits of integration, so NIntegrate was being called before a value was plugged into $r$.

I was able to get a solution to the problem in MM version 12.2 with:

    fun[rho_, r_] := Times[r, Integrate[Times[rho, p, p], {p, 0, r}]];
    sol = NDSolve[{R'[r] == D[fun[R[r], r], r], R[0] == 1}, R, {r, 0, 1}][[1,1,2]];
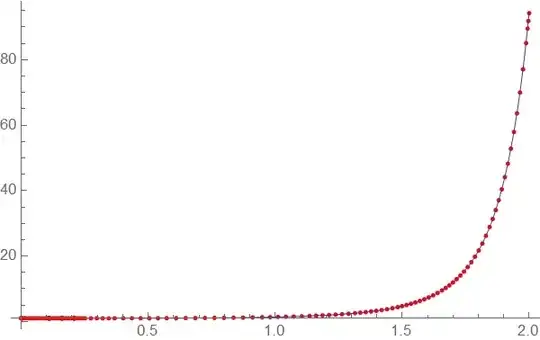
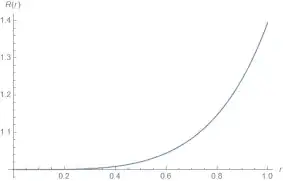
    Plot[sol[r], {r, 0, 1}]

gives a plot that looks like:

I would note that the solution seems to be faster without using NumericQ on the function, but depending on your application, you may or may not wish to keep it there.

I was able to get two different analytical solutions, the first being:

    a1 = DSolve[{R'[r] == D[r * Integrate[q * q * R[q], {q, 0, r}], r], R[0] == p}, R[r], r]

and a more refined version over the unit interval:

    a2 = DSolve[{R'[r] == D[r * Integrate[q * q * R[q], {q, 0, r}], r], R[0] == p}, R[r], {r, 0, 1}]

yielding the expressions: \begin{equation} R\left( r\right)=\frac{1}{4\sqrt{2}} e^{\frac{r^{4}}{4}}p\left[ r\;\Gamma\left( -\frac{1}{4}\right) -\left( r^{4}\right)^{\frac{1}{4}} \Gamma\left( -\frac{1}{4}, \frac{r^{4}}{4}\right) \right] \end{equation}

where $\Gamma\left(\cdot\right)$ and $\Gamma\left(\cdot,\cdot\right)$ are intended to mean the gamma and upper-incomplete gamma functions respectively, and on the unit interval:

\begin{equation} R\left(r\right)=\frac{1}{4}e^{\frac{r^{4}}{4}}p\left[E_{5/4}\left(\frac{r^{4}}{4}\right) + 2\sqrt{2}\;r\;\Gamma\left(\frac{3}{4}\right)\right] \end{equation}

where $E_{n}$ is the exponential integral function.

To be true(er) to the original problem though, I was able to use:

    mfun[rho_?NumericQ, r_?NumericQ] := r NIntegrate[rho r1^2, {r1,0,r}];
    msol = NDSolve[{R'[r] == D[mfun[R[r], r], r], R[0] == 1}, R, {r,0,1}][[1,1,2]]

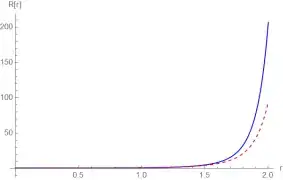
which when plotted gives the same visual as shown above.

Answer 2

If the integral is assumed to be inrooted, I can think out 2 approaches. First one is the relaxation method:

intfunc[R_, r_?NumericQ] := 
  NIntegrate[r1^2*R[r1], {r1, 0, r}, Method -> {Automatic, SymbolicProcessing -> 0}];
sollst = NestList[
    NDSolveValue[{R'[r] == intfunc[#, r] + r^3 #[r], R[0] == 1}, R, {r, 0, 2}] &, 
    Identity, 10]; // AbsoluteTiming
(* {0.402924, Null} *)
aplot = Plot[(E^(r^4/4) (-r Gamma[-(1/4)] + (r^4)^(1/4) Gamma[-(1/4), r^4/4]))/(
  4 Sqrt[2]), {r, 0, 2}, PlotRange -> All];
ListPlot[sollst[[-1]], PlotRange -> All, PlotStyle -> Red]~Show~aplot

The next one is finite difference method (FDM), which is harder to code but more efficient at least in this case. I'll use pdetoae to facilatate the generation of difference equations:

Clear@int
int[expr_, {var_, 0, rlst_List}] := int[expr, {var, 0, #}] & /@ rlst
int[expr_, {var_, 0, r_?NumericQ}] := 
 With[{pos = Rescale[r, domain, {1, points}]}, 
  trap[Function @@ {var, expr}, grid[[;; pos]]]]
(* trapezoidal rule: *)
trap[f_, grid_] := 
  With[{h = -Subtract @@ domain/(points - 1)}, 
   h (Total[f /@ grid] - 1/2 (f@grid[[1]] + f@grid[[-1]]))];
eq = R'[r] == D[r intmid[r], r];
ic = R[0] == 1;
points = 80;
domain = {0, 2};
grid = Array[# &, points, domain];
difforder = 4;
(* Definition of pdetoae isn't included in this post,
   please find it in the link above. *)
ptoafunc = pdetoae[{R, intmid}[r], grid, difforder];
ae = Rest@ptoafunc[eq] /. Thread[ptoafunc[intmid[r]] -> int[r1^2 R[r1], {r1, 0, grid}]];
guess[r_] = 1;
nsol = ListInterpolation[
    FindRoot[Flatten@{ae, ic}, 
      Table[{R@r, guess[r]}, {r, grid}]][[All, -1]], {grid}]; // AbsoluteTiming
(* {0.103995, Null} *)
ListPlot[nsol, PlotRange -> All, PlotStyle -> Red]~Show~aplot

Answer 3

extended

If I understand the question right, OP is looking for a numerical solution where integral isn't known analytically.

First we need a function definition of the integral part, where a function ip is passed as argument.

int[ip_][r_?NumericQ] :=Module[{u}, NIntegrate[u^2 ip[u], {u, 0, r}]  ]

Differentiating the integralequation "manually" (don't know why NDSolve can't handle D[r int[Function[{r}, R[r]]][r ],r] ) gives the ode

RR = NDSolveValue[{R'[r] == int[Function[{r}, R[r]]][r ] + r^3 R[r],R[0] == 1}, R, {r, 0, 2}]
Plot[RR[r], {r, 0, 1}]

The solution agrees quite well (also in the extended domain 0<r<2 , see @xzczd comment, Thanks) with the analytical one in @Nathan White`s answer:

sol=DSolve[{R'[r] == D[r * Integrate[q * q * R[q], {q, 0, r}], r], R[0] == 1}, R[r],  r ]
Plot[{RR[r], R[r] /. sol}, {r, 0, 2}, AxesLabel -> {"r","R[r]"},PlotRange -> All, PlotStyle -> {Blue, {Dashed, Red}}]