FourierSeries for rational function looks wrong

Question

Bug introduced in Version 8 or earlier, and persisting through 12.1.

I have the following code:

ser[x_] = FourierSeries[(π^2 + a)/(3 x^2 + a), x, 10] // N // Chop

It gives me some series, which I then try to plot. And surprisingly, the result isn't even similar to the function I passed to FourierSeries[]: for comparison, I've used this code:

Plot[{ser[x], 1000 (π^2 + a)/(3 x^2 + a)}, {x, -π, π}]

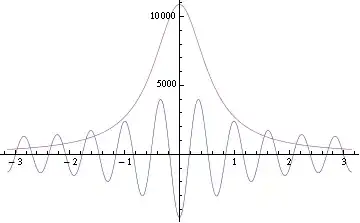
output

Fourier transform for function given in documentation works correctly, while for this one doesn't. I've tried using directly the formula given in documentation as default formula (used NIntegrate[]), and that gives me expected results.
What have I done wrong? Is this a bug?

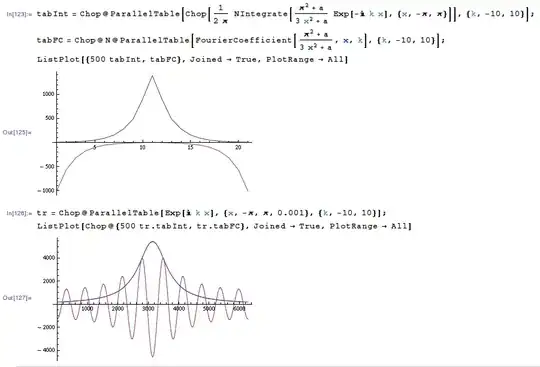
Addition to answer comments: some more code

As one can see, the Fourier coefficients computed via NIntegrate[] are quite different from ones generated by FourierCoefficient[].

Update:
As pointed in comments, setting GenerateConditions->True appears to yield correct result, not generating any conditions though. Why should this be needed?

No it's not. I've tried using normal NIntegrate[] to the same order, it gives correct shape. — Ruslan, May 03 '13 at 20:36
Actually FourierCosSeries works fine. Are you sure it can't be the feature of the Laplace distribution for its series to behave like this? — swish, May 03 '13 at 20:43
@swish yes, see update. It's Fourier coefficients which look wrong, not the function behavior. — Ruslan, May 03 '13 at 20:53
Yeah, I figured that. Integrate does also yield a different coefficient, both in v8 and v9. — Sjoerd C. de Vries, May 03 '13 at 22:42
Try GenerateConditions -> True, then it will yield the correct result somehow, without any actual conditions generated. And maybe edit you question asking why FourierCoefficient does this. — swish, May 04 '13 at 00:34
Hmm, funny. What's your default setting for FourierParameters? — J. M.'s missing motivation, May 04 '13 at 01:01
@J.M. Defaults are, as said in documentation, {1,1}. Setting them explicitly doesn't change results. Neither does {1,-2Pi} change behavior. — Ruslan, May 04 '13 at 07:59
The problem could be boiled down to this function 1/(x^2 + 1) - no need to put a and Pi there - just confuses things. It's a bell function. To realize the problem one should compare to another bell, like Sech[x]. 5 terms or even 3 will be enough. No need to go numeric either. — Vitaliy Kaurov, May 11 '13 at 06:23

David E Speyer · Accepted Answer · 2013-05-15T16:40:19.247

Something strange is going on here. Here is a computation which illustrates the issue without some of the extraneous aspects.

wrong = FourierCoefficient[1/(x^2 + 1), x, 1]

The variable wrong now contains what FourierCoefficient thinks is the coefficient of $e^{i x}$ in the fourier series of $1/(x^2+1)$. According to the documentation for FourierCoefficient (v. 8) "The $n^{th}$ coefficient in the Fourier series of $f(t)$ is by default given by $\frac{1}{2 \pi} \int_{- \pi}^{\pi} f(t) e^{-int} dt$." In other words, wrong should be equal to $\frac{1}{2 \pi} \int_{- \pi}^{\pi} \frac{e^{-it}}{1+t^2} dt$. Let's put that integral directly into Mathematica:

right = Integrate[E^(-I x)/(x^2 + 1), {x, -Pi, Pi}] / (2 Pi)

So we should have wrong == right. In fact:

Simplify[wrong - right]

(* Output -E/2 *)

It looks like FourierCoefficient[] is computing $\int_{- \pi}^{\pi} \frac{e^{-i t}}{t^2+1} dt$ along the wrong path in the complex plane. If you think of $\frac{e^{-i t}}{t^2+1}$ as a function of a complex variable $t$, it has poles at $\pm i$. The value of the integral will be different depending on whether you take a path that goes over both poles, under both or (the correct choice) along the real axis between the poles. If we go over the pole at $i$ when we should have gone under, we pick up an extra $(2 \pi i) R$ where $R$ is the residue at $i$.

Residue[E^(-I*t)/(t^2 + 1), {t, I}]

(* Output - I*E/2 *)

So $R= -ie/2$, making the integral off by $- (2 \pi i) (i e/2) = \pi e$. Then we have a $\frac{1}{2 \pi}$ in front of the integral, so our final answer is off by $e/2$.

The error even affects the cognate function FourierCoefficient[]. Very suspicious... — J. M.'s missing motivation, May 15 '13 at 16:37
Edited my example to use FourierCoefficient, so that I don't have to muck around in the interior of FourierSeries output. Thanks! — David E Speyer, May 15 '13 at 16:43
FourierCoefficient[1/(x^2 + 1), x, 1, Assumptions -> -Pi < x < Pi] gives the correct answer. — David E Speyer, May 15 '13 at 17:12
Now that's just weird. Here we thought we don't have to add the assumption that the integration variable is within the integration interval... :D — J. M.'s missing motivation, May 15 '13 at 17:14
Quite an interesting answer, thanks. Also, setting Assumptions->Element[x, Reals] appears enough for it to work. — Ruslan, May 15 '13 at 20:22

FourierSeries for rational function looks wrong

1 Answers1

Linked