Plot the intersection of random half-spaces

Question

The code

n=30; (*number of points *)
points = RandomPoint[Sphere[],n]; (*points uniformly distributed on the unit sphere*)
p = ImplicitRegion[Table[points[[i]].{x,y,z}<=1,{i,1,n}],{x,y,z}]; (* intersection of corresponding half spaces *)
Region[p,PlotTheme->"Detailed"]

produces the following picture. It represents the intersection of 30 half spaces whose supporting hyperplanes are tangent to the sphere at random points.

The edges of that polyhedron are messed up. Is there something I can do to get a better picture ?

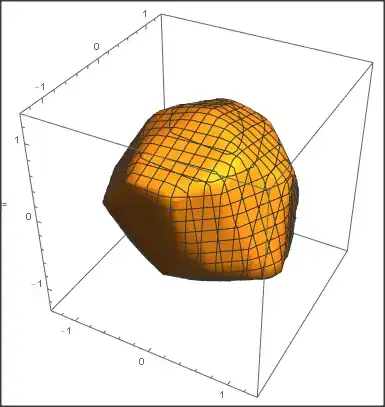
You can improve on it for example like this: BoundaryDiscretizeRegion[p, MaxCellMeasure -> 0.001]. Decrease the MaxCellMeasure for a more accurate result. I will not post this as an answer as I am not personally satisfied with it. This will cause all flat faces of the region to be broken into a very large number of tiny cells as well. I would hope for a solution that uses the smallest possible number of faces. — Szabolcs, May 17 '21 at 09:52
Out of curiosity, is this related to a Voronoi mesh? It looks quite similar. (I note that there is no 3D implementation of a Voronoi mesh in WL) — Carl Lange, May 17 '21 at 12:26
@CarlLange I don't think it is related to Voronoi mesh. In general the facet of a Voronoi cell are not all tangent to one sphere. — Gilles Bonnet, May 17 '21 at 15:14
Another excellent answer which provides even more than I have asked here: https://mathematica.stackexchange.com/a/14774/10686 — Gilles Bonnet, May 17 '21 at 15:15
Related: why-clipplane-show-a-hollow-object-for-a-filled-object , find-the-3d-region-containing-the-origin-bounded-by-given-planes — chyanog, Apr 29 '22 at 08:49

cvgmt · Accepted Answer · 2021-05-17T11:06:17.877

For a given j,We can use Hyperplane[points[[j]], points[[j]]] to represent the plane which tangent to the unit sphere at point points[[j]]. Then we use another n-1 HalfSpace to cut such plane and get one of such face.

n = 30;
points = RandomPoint[Sphere[], n];
faces = Table[
   RegionIntersection[Hyperplane[points[[j]], points[[j]]], 
    Sequence @@ 
     Table[HalfSpace[points[[i]], points[[i]]], {i, 
       Complement[Range[n], {j}]}]], {j, 1, n}];
DiscretizeRegion[#, MaxCellMeasure -> 10^-6] & /@ faces // Show

score 4 · Answer 2 · answered May 17 '21 at 10:07

4

Region is a rather quick and dirty plotting routine. More elaborate is RegionPlot:

n = 30;

SeedRandom[1];
points = RandomPoint[Sphere[], n]; p = 
 ImplicitRegion[
  Table[points[[i]].{x, y, z} <= 1, {i, 1, n}], {x, y, z}];
d = 1.3;
RegionPlot3D[{x, y, z} \[Element] p, {x, -d, d}, {y, -d, d}, {z, -d, 
  d}, PlotPoints -> 20]

answered May 17 '21 at 10:07

Daniel Huber

51,463
1
23
57

The PlotPoints->150 option improves the result though slowing down the execution. – user64494 May 17 '21 at 10:20
1

@user64494 - it is more efficient to use a combination of increasing both PlotPoints and MaxRecursion rather than depending solely on PlotPoints. For example, compare the results and timing for PlotPoints->100 versus PlotPoints -> 50, MaxRecursion -> 6 – Bob Hanlon May 17 '21 at 13:59

score 3 · Answer 3 · answered Apr 29 '22 at 08:43

3

Using BoundaryDisctizeGraphics to discretize the HalfSpace first , then use RegionIntersection.

n = 30;
SeedRandom[1];
points = RandomPoint[Sphere[], n];
AbsoluteTiming[reg = BoundaryDiscretizeGraphics[HalfSpace[#, 1], PlotRange -> 2] & /@
  points // RegionIntersection]

Length[faces = MeshPrimitives[reg, 2]]

30

answered Apr 29 '22 at 08:43

chyanog

15,542
3
40
78

Nice shot for BoundaryDisctizeGraphics with HalfSpace! – Αλέξανδρος Ζεγγ May 14 '22 at 09:37

Plot the intersection of random half-spaces

3 Answers3