I have that $(x,y)\in S^1$, i.e. on the sphere, and in Mathematica, the ODE system
f = x^3 - x y^2 + y^3 ;
xdot = x (-x + f);
ydot = y (x - y + f);
vector = {xdot, ydot};
How can I plot the phase portrait on $S^1$?
I do not know how to plot this in Mathematica.
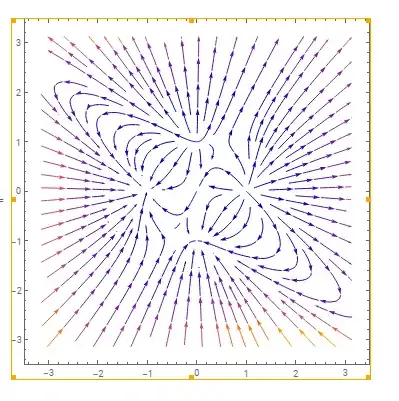
Of course there is the StreamPlot function and I can do
StreamPlot[{ x (-x + f), y (x - y + f)},{x,-Pi,Pi},{y,-Pi,Pi}]
which gives
But I am only interested in the dynamics which happens directly on $S^1$.
How can I filter that out to get something like sketched here: