Asymptotic[] Doesn't Actually Compute

Question

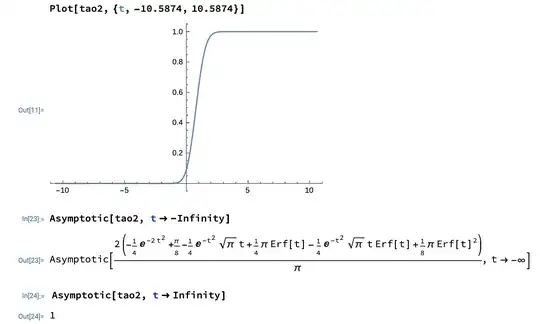
I ran into this problem while studying the asymptotic behavior of a probability distribution function called tao2. It computes correctly at positive infinity but doesn't actually compute at negative infinity. Instead, Mathematica simply spits out the input. Is there any way to fix this?

For reference,

tao2 = (2*(-(1/4)/E^(2*t^2)+Pi/8-((1/4)*Sqrt[Pi]*t)/E^t^2+(1/4)*Pi*Erf[t]
  -((1/4)*Sqrt[Pi]*t*Erf[t])/E^t^2+(1/8)*Pi*Erf[t]^2))/Pi

Update 1: Asymptotic[] works when I separate tau2 into two parts and compute separately (one contains all terms involving the error function, another contains all other terms). However, these two parts add up to 0, while I expect to see E^(-2*t^2)/t^2 times some constant.

Update 2: As Bob Hanlon suggested, the expanded form of the tao function is indeed more suitable for computation. However, when using both the original form and the expanded form on a tester function (called tao1), the two methods produce different results. Here

tao1 = (1/2)*(1+Erf[t])

Please provide the Mathematica code (InputForm) for the definition of tao2 that can be copy and pasted. — Bob Hanlon, May 19 '21 at 17:31
Use either Limit[tao2, t -> -Infinity] or Series[tao2, {t, -Infinity, 1}] // Normal Both evaluate to 0 — Bob Hanlon, May 19 '21 at 17:46
Interestingly, Asymptotic[FullSimplify@tao2, t -> -Infinity] seems to work. — thorimur, May 19 '21 at 18:59
@thorimur I just tried that but it gave the (simplified) expression of tau2. Do you mind sharing the result you got? — Jade Peng, May 19 '21 at 19:23
Oh, I see. yes, you're right, that's simply tau2 in a different form very weird. — thorimur, May 19 '21 at 19:28

Bob Hanlon · Accepted Answer · 2021-05-20T04:10:06.770

5

tao2 = (2*(-(1/4)/E^(2*t^2) + 
       Pi/8 - ((1/4)*Sqrt[Pi]*t)/E^t^2 + (1/4)*Pi*Erf[t] - 
        ((1/4)*Sqrt[Pi]*t*Erf[t])/E^t^2 + (1/8)*Pi*Erf[t]^2))/Pi;

Expanding tao2 and calculating the Asymptotic for each term

Asymptotic[#, t -> -Infinity] & /@ (tao2 // Expand)
(* -(E^(-2 t^2)/(2 π)) *)
Limit[%, t -> -Infinity]
(* 0 *)

EDIT: Similarly, for the other side

Asymptotic[#, t -> Infinity] & /@ (tao2 // Expand)
(* 1 - E^(-2 t^2)/(2 π) - (E^-t^2 t)/Sqrt[π] *)
Limit[%, t -> Infinity]
(* 1 *)

EDIT 2: For the tao1 example:

Clear["Global`*"]
tao1 = (1/2)*(1 + Erf[t]);
Asymptotic[tao1, t -> -Infinity]
(* -(E^-t^2/(2 Sqrt[π] t)) *)
Asymptotic[#, t -> -Infinity] & /@ (tao1 // Expand)
(* 0 *)

To get the same result mapping onto the expanded expression, the option SeriesTermGoal is needed.

Asymptotic[#, t -> -Infinity, SeriesTermGoal -> 2] & /@ 
 (tao1 // Expand)
(* -(E^-t^2/(2 Sqrt[π] t)) *)
Limit[%, t -> -Infinity]
(* 0 *)

edited May 20 '21 at 04:10

answered May 19 '21 at 20:17

Bob Hanlon

157,611
7
77
198

Thanks, it works! Do you mind sharing the reasoning behind it, i.e. why the expanded form is more suitable for computation in this case? – Jade Peng May 19 '21 at 22:45
3

Expand produces an expression with the Head Plus. The individual terms are simpler and easier for Asymptotic to process. Mapping onto the Plus automatically sums the individually processed terms. This is analogous to doing complicated integrations that don't directly evaluate with Integrate[#, {x, x0, xf}] & /@ (expr // Expand) – Bob Hanlon May 19 '21 at 22:58
That really helps. Thanks so much! – Jade Peng May 20 '21 at 01:02
On a side note, I tried both the original form and with Expand on a tester function, but they different output (as shown in the modified question prompt). Should we expect them to be the same? – Jade Peng May 20 '21 at 02:25

Asymptotic[] Doesn't Actually Compute

1 Answers1