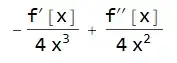1

I have this differential operator $$\frac{d^2}{d y^2}\qquad (1)$$ I want to make a change of variable $y=x^2$ in $(1)$ so that I get this differential operator $$ \frac{1}{4 x^2} \frac{d^2 }{d x^2}-\frac{1}{4 x^3}\frac{d}{d x} \qquad (2)$$

How can I ask Mathematica to do this?

Phys96
  • 361
  • 1
  • 6
  • 1
    Related: https://mathematica.stackexchange.com/questions/80241/analogue-for-maples-dchange-change-of-variables-in-differential-expressions – Michael E2 May 20 '21 at 18:33
  • 1
    Do you want the result to be a function you can apply to an expression? – Michael E2 May 20 '21 at 18:34
  • 1
    @MichaelE2 No, I want to apply this operator to a function. – Phys96 May 20 '21 at 20:20
  • 1
    From a programming point of view, doesn't "apply this operator" mean you want the operator to be function that takes a function as an argument and returns the desired derivative? By "function" do you mean $f$ or an expression like $f(y)$? These are different, both in mathematics and in coding. Please give paradigm of how you want the code to work, in terms of input and output code. TeX/math is confusing. (Btw, don't you mean $f(x^2)$ in (2)?) – Michael E2 May 20 '21 at 21:05
  • @MichaelE2 I meant exactly what Alexi 's answer says. – Phys96 May 20 '21 at 22:12

2 Answers2

5

Try this:

Clear[f];
D[f[y], {y, 2}] /. f -> (f[#^(1/2)] &) /. y -> x^2 // 
  Simplify[#, x > 0] & // Expand

(*  -(Derivative[1][f][x]/(4 x^3)) + (f^[Prime][Prime])[x]/(4 x^2)  *)

enter image description here

Have fun!

Alexei Boulbitch
  • 39,397
  • 2
  • 47
  • 96
  • 1
    Shouldn't the correct answer have f'[x^2] etc.? – Michael E2 May 20 '21 at 21:22
  • @MichaelE2 No, the result is correct. – Phys96 May 20 '21 at 22:13
  • 1
    @Phys96 Why does $f(y)$ become $f(x)$, when $y$ is replaced by $x^2$? That seems quite wrong. – Michael E2 May 20 '21 at 22:15
  • @MichaelE2 I will write in detail later, maybe it is my bad in writing the question, Indeed, here, we apply the change of variable $y=f(x)=x^2$ – Phys96 May 21 '21 at 06:51
  • @MichaelE2 I think that formally you are right. Implicitly, f(x) is another function, not equal to f(y). This may later cause errors in calculations. Correctly would be to introduce a different function g(x)=f(x^2) and formulate everything for the latter: D[f[y], {y, 2}] /. f -> (g[#^(1/2)] &) /. y -> x^2. – Alexei Boulbitch May 21 '21 at 08:47
2

Here's a counterexample to show that (1) applied to f[y] is not equivalent to (2) applied to f[x] under the substitution y == x^2, as it was stated in the OP in a previous edit and claimed in a comment:

Block[{f = Cos},
 {D[f[y], {y, 2}] /. y -> x^2,
   1/(4 x^2) D[f[x], {x, 2}] - 1/(4 x^3) D[f[x], x] // Simplify,
   1/(4 x^2) D[f[x^2], {x, 2}] - 1/(4 x^3) D[f[x^2], x] // Simplify
   } // Simplify]
Michael E2
  • 235,386
  • 17
  • 334
  • 747