Given 3 point, search the center of the circle through these points.
The center of the circle must lay in the same plane as p1,p2,p3, therefore we can write:
SeedRandom[12];
{p1, p2, p3} = RandomReal[{-1, 1}, {3, 3}];
c = p3 + l1 (p1 - p3) + l2 (p2 - p3);
with the center c and unknowns l1 and l2. These are determined by the condition that the distance to the center is the same for all points:
dis = (# - c) . (# - c) & /@ {p1, p2, p3};
eq = dis[[1]] == dis[[2]] == dis[[3]] // Simplify // Chop;
We solve these equations for l1 and l2 and get the center:
sol = Solve[eq, {l1, l2}][[1]] // Chop;
center = c /. sol /. l1 -> 1 // Simplify;
the distance from the points to the center:
Norm[# - center] & /@ {p1, p2, p3}
(* {0.833413, 0.833413, 0.833413} *)
Graphics3D[{
Cylinder[{center, center + 0.001 Cross[p1 - p3, p2 - p3]},
Norm[p1 - center]], PointSize[0.03], Blue, Point[{p1, p2, p3}],
Red, Point[center]
}]


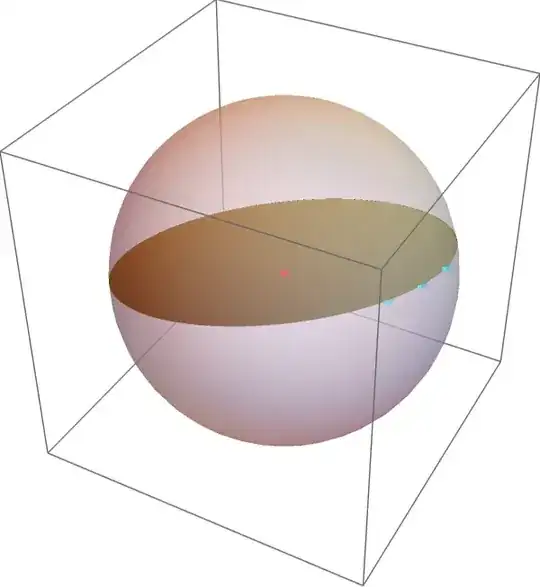

reg = HighlightMesh[ DiscretizeRegion@ RegionIntersection[InfinitePlane[Array[p, 3]], Sphere[{x, y, z}, r] /. sol], {Style[1, {Thick, Brown}], Style[0, None]}];– cvgmt May 25 '21 at 13:11