Gradient of the numerical solution of a PDE

Question

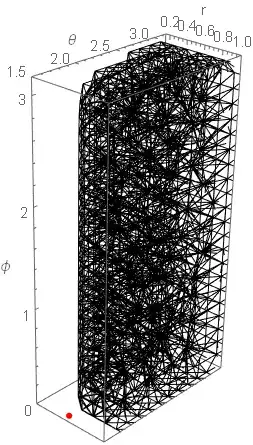
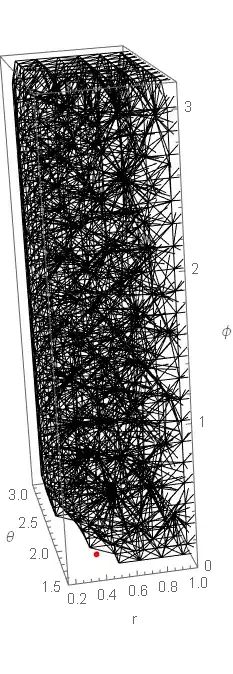
Solving the following PDE, defined in the same domain of a previous question:

p = 0.2;
Pe = 20;
<< NDSolve`FEM`
boundaries = {-r + 
    1/2 (Sqrt[2] Sqrt[Cos[2 \[Theta]] (1 - p)^2 + 2 p + 1 - p^2] + 
       2 Cos[\[Theta]] (1 - p)), 
   r - 8, -\[Theta] + Pi/2, \[Theta] - Pi, -\[Phi], \[Phi] - Pi};
\[CapitalOmega] = 
  ToElementMesh[
   ImplicitRegion[
    And @@ (# <= 0 & /@ boundaries), {r, \[Theta], \[Phi]}], 
   "MaxBoundaryCellMeasure" -> 0.04];
Show[\[CapitalOmega][
  "Wireframe"["MeshElement" -> "MeshElements", Boxed -> True]], 
 AxesLabel -> {"r", "\[Theta]", "\[Phi]"}, 
 PlotRange -> {{0.15, 1}, {1.5, 3.16}, {0, 3.16}}]

and

sol = NDSolveValue[{Sin[\[Theta]] Cos[\[Phi]] D[
       T[r, \[Theta], \[Phi]], r] + (Cos[\[Theta]] Cos[\[Phi]])/
      r D[T[r, \[Theta], \[Phi]], \[Theta]] - 
     1/r D[T[r, \[Theta], \[Phi]], \[Phi]] == 
    1/Pe (1/r^2 D[r^2 D[T[r, \[Theta], \[Phi]], r], r] + 
       1/(r^2 Sin[\[Theta]])
         D[Sin[\[Theta]] D[
           T[r, \[Theta], \[Phi]], \[Theta]], \[Theta]] + 
       1/(r^2 (Sin[\[Theta]])^2)
         D[T[r, \[Theta], \[Phi]], {\[Phi], 2}]), {DirichletCondition[
     T[r, \[Theta], \[Phi]] == 1., boundaries[[1]] == 0.],
    DirichletCondition[T[r, \[Theta], \[Phi]] == 0., 
     boundaries[[2]] == 0.]}}, 
  T, {r, \[Theta], \[Phi]} \[Element] \[CapitalOmega]]

I noticed a strange behavior of the solution. For example:

\[Theta]1 = 0.6 Pi;
sol[1/2 (Sqrt[2] Sqrt[Cos[2 \[Theta]1] (1 - p)^2 + 2 p + 1 - p^2] + 
    2 Cos[\[Theta]1] (1 - p)), \[Theta]1, 0 Pi]

or

sol[0.5, 0.5 Pi, 0 Pi]

give: InterpolatingFunction::dmval: Input value {.....} lies outside the range of data in the interpolating function. Extrapolation will be used, though the input values are inside the domain of the solution. Furthermore, the plot of the solution for small values of \[Phi]] looks fine:

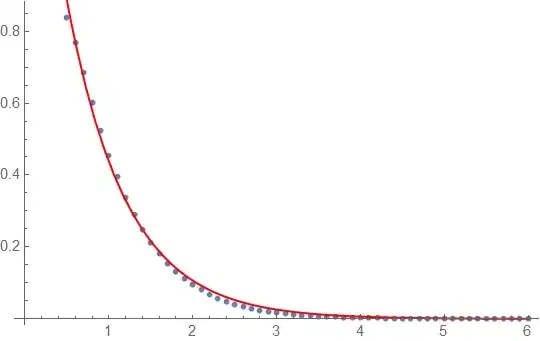
Plot[sol[r, 0.6 Pi, 0.0 Pi], {r, 0.4025, 8}, Frame -> True, 
 PlotRange -> {{0.15, 8}, {-0.1, 1.2}}]

but

Plot[sol[r, 0.6 Pi, 0.8 Pi], {r, 0.4025, 8}, Frame -> True, 
 PlotRange -> {{0.15, 8}, {-0.1, 1.2}}]

gives:

Things are even worse with the derivative of the solution, that I need to find the gradient of T on the curved portion of the domain, the final aim being to calculate the flow of the grad of T through the spherical cap. E.g.,

Dr[r_, \[Theta]_, \[Phi]_] = D[sol[r, \[Theta], \[Phi]], r]
Plot[Dr[r, 0.6 Pi, 0.0 Pi], {r, 0.403, 8}, Frame -> True, 
 PlotRange -> {{0.15, 6}, {-1.6, 0.1}}]

gives:

Things seem to improve if the MaxBoundaryCellMeasure is decreased, at the cost of the computational time however, but the problems on the derivative still remain. I am grateful for any help.

Answer 1

Your post contains three different questions.

The first is why you get the warning "Input value {.....} lies outside the range of data in the interpolating function?"

The answer is that this point, indeed, lies outside the mesh. One can make this sure by plotting the mesh simultaneously with the point in question:

Show[{
  \[CapitalOmega][
   "Wireframe"["MeshElement" -> "MeshElements", Boxed -> True]],
  Graphics3D[{Red, PointSize[0.03], Point[{0.5, 0.5 Pi, 0 Pi}]}]
  }, Axes -> True, AxesLabel -> {"r", "\[Theta]", "\[Phi]"}, 
 PlotRange -> {{0.15, 1}, {1.5, 3.16}, {0, 3.16}}]

yielding the following image:

Here the red dot indicates the point {0.5, 0.5 Pi, 0 Pi}. One can see that it is outside the mesh built in the previous code.

Later edit: Also the point

{1/2 (Sqrt[2] Sqrt[Cos[2 \[Theta]1] (1 - p)^2 + 2 p + 1 - p^2] + 
     2 Cos[\[Theta]1] (1 - p)), \[Theta]1, 0.0 Pi} /. \[Theta]1 ->0.6 Pi
(*  {0.40172, 1.88496, 0.}  *)

lies outside the mesh. To make it clear one needs again draw the mesh together with this point:

Show[{\[CapitalOmega][
   "Wireframe"["MeshElement" -> "MeshElements", Boxed -> True]],
Graphics3D[{Red, PointSize[0.03], 
    Point[{1/
         2 (Sqrt[2] Sqrt[
            Cos[2 [Theta]1] (1 - p)^2 + 2 p + 1 - p^2] + 
          2 Cos[[Theta]1] (1 - p)), [Theta]1, 
       0.0 Pi}] /. [Theta]1 -> 0.6 Pi}]},
Axes -> True, AxesLabel -> {"r", "[Theta]", "[Phi]"}, 
 PlotRange -> {{0.15, 1}, {1.5, 3.16}, {0, 3.16}}]

and then turn the whole image against the clock. The image is shown below:

One can see that this point also lies outside the mesh. It only seemed covered by the mesh in the case of the default ViewPoint.

Continuation:

The second question is what's wrong with your second plot.

Indeed, it looks incorrectly. When I evaluated your code I got the message:

"The computed Peclet number is 3.568... and is larger than the mesh order (2), and the result may not be stable. Refining the mesh or adding artificial diffusion may help."

In other words, the first attempt I would do in such a case would be mesh refinement. Other steps proposed by the message I would only undertake if this first attempt will not help.

The third question is why the last plot looks so noisy. The reason, I think, is that here the derivative of the interpolation function is calculated numerically. Such a behavior is typical for the numeric derivatives and always takes place if after the numerical solution of a differential equation one looks for its derivative.

I think there could be several workarounds. In such a case, I would do here as follows. Using the solution I would create a list along the direction you need to get the gradient and then fit it by some analytic function. In the case under the study it can be as follows:

lst = Table[{r, sol[r, 0.6 Pi, 0.0 Pi]}, {r, 0.5, 6, 0.1}];
model = a*Exp[-b*r];
ff = FindFit[lst, model, {a, b}, r]
(*  {a -> 1.79379, b -> 1.41339}  *)

Let us visually check the fitting quality:

Show[{
  ListPlot[lst],
  Plot[model /. ff, {r, 0.5, 6}, PlotStyle -> Red, PlotRange -> All]
  }]

with the following effect

If you are satisfied with the quality (I would be reasonably satisfied) you can find the derivative

D[model /. ff, r]
(*  -2.53532 E^(-1.41339 r)  *)

and plot it:

Plot[-2.54 E^(-1.4 r), {r, 0.5, 6}, PlotStyle -> Blue,PlotRange -> All]

which I hope looks as expected.

Maybe, there are also other, better workarounds.

Have fun!