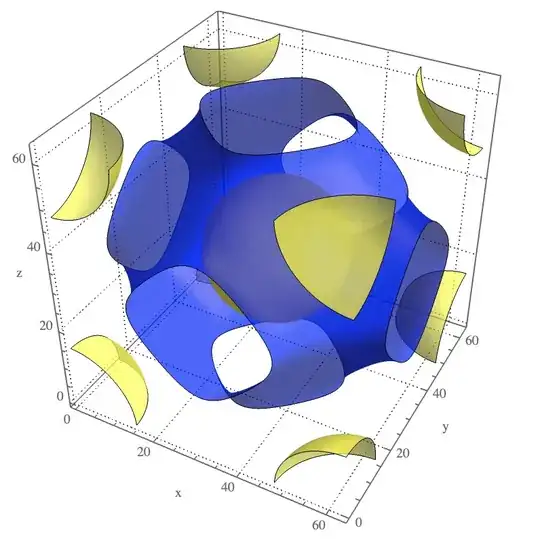
Like the title indicates, how could I achieve this. Normally what I did for a closed surface is as follows:
RegionMeasure[RegionBoundary[BoundaryDiscretizeGraphics[a]]]
where a is an output from ListContourPlot3D. However, this fails when applied on a surface that is not closed. For example, if I want to calculate the total area of all the yellow (or the blue) surfaces in the following plot (again given by ListContourPlot3D), I wonder what the easiest possible way to do it.
- 437
- 2
- 8
-
3can you show your full code please ! – nufaie Jun 02 '21 at 21:26
1 Answers
Following @Mr. Wizards answer here, you could extract the individual polygons from each graphics group and total up the areas. Note that some areas are undefined due to probably degenerate polygons. As long as you can tolerate the loss of a few polygons, the following workflow may work:
(* Example from documentation *)
a = ListContourPlot3D[
Table[x^2 + y^2 - z^2, {x, -2, 2, 0.2}, {y, -2, 2, 0.2}, {z, -2, 2,
0.2}], Contours -> 5, Mesh -> All, PlotLegends -> "Expressions"]
(* extract info from plot *)
poly = Cases[Normal[a],
GraphicsGroup[g_] :>
Cases[g, Polygon[p_, __] :> Polygon[p], -4], -5];
colors = Cases[
a, {___, c_Directive, __GraphicsGroup} :>
ColorConvert[c, RGBColor], Infinity];
(* calculate areas *)
areas = DeleteCases[Area /@ poly[[#]], Undefined] & /@
Range[poly // Length];
Print["Areas of each surface group"];
AssociationThread[Range[poly // Length], Total /@ areas]
AssociationThread[colors, Total /@ areas]
Print["Display groups 1 and 2"];
Graphics3D[{Opacity[0.75], EdgeForm[Black], colors[[1]], poly[[1]],
colors[[2]], poly[[2]]}]
Response to the updated question
The question does not provide a Minimal Working Example (MWE), but it does provide an example of a polygon that fails. If we examine the points, we see that they are not coplanar (a requirement for a valid Polygonregion).
pts = {{10.`, 22.8529`, 4.`}, {10.8562`, 22.`, 4.`}, {11.`, 22.`,
4.34981`}, {11.`, 22.2385`, 5.`}, {10.2474`, 23.`, 5.`}, {10.`,
23.`, 4.34491`}};
CoplanarPoints[pts]
Area@Polygon@pts
One way to avoid the coplanar issue is to split all the polygons into triangles. The following functions (non-optimize) will split the higher-order polygons into triangles.
Clear[polySplit]
polySplit[p_] := Module[{pts = p[[1]], l, m},
l = Length@pts;
m = Mean@pts;
pts = Join[pts, {First@pts}];
Polygon[{m, pts[[#]], pts[[# + 1]]}] & /@ Range[l]
]
Clear[splitGroup]
splitGroup[pgrp_] :=
Module[{sides, len, tripos, polypos, tris, areas, exclude, keep},
sides = Length[#[[1]]] & /@ pgrp;
len = Length@sides;
tripos = Position[sides, 3] // Flatten;
tris = pgrp[[tripos]];
polypos = Complement[Range[len], tripos];
tris = Join[tris, polySplit[#] & /@ pgrp[[polypos]] // Flatten];
areas = Area /@ tris;
len = Length@areas;
exclude = Flatten[Position[areas, Undefined]];
keep = Complement[Range[len], exclude];
<|"tris" -> tris, "areas" -> areas[[keep]],
"totalArea" -> Total[areas[[keep]]]|>]
The following workflow will split the polygons into their primitive forms and calculate the areas.
(* Example from documentation *)
a = ListContourPlot3D[
Table[x^2 + y^2 - z^2, {x, -2, 2, 0.2}, {y, -2, 2, 0.2}, {z, -2, 2,
0.2}], Contours -> 5(*,Mesh\[Rule]All*),
PlotLegends -> "Expressions"];
(* extract info from plot *)
poly = Cases[Normal[a],
GraphicsGroup[g_] :>
Cases[g, Polygon[p_, __] :> Polygon[p], -4], -5];
colors = Cases[
a, {___, c_Directive, __GraphicsGroup} :>
ColorConvert[c, RGBColor], Infinity];
(* calculate areas *)
Print["Areas of each surface group"];
groups = splitGroup /@ poly;
AssociationThread[colors, #["totalArea"] & /@ groups]
Print["Display groups 1 and 2"];
Graphics3D[{Opacity[0.75], EdgeForm[Black], colors[[1]],
groups[[1]]["tris"], colors[[2]], groups[[2]]["tris"]}]
These results agree with the previous results.
- 16,346
- 1
- 34
- 58
-
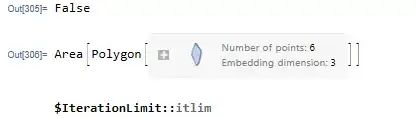
Thanks for the solution. However, when I implemented this I found that
Area/@poly[[#]]doesn't work on all of the polygons in my case. For example, this may result in an actual value corresponding to the area for some polygons, but it just returnsArea[polygon[]]for the others. I also encounter this in some other cases. Do you know why this happens? (Please see the added screenshot for this issue) – Dennis Jun 03 '21 at 18:15 -
@Dennis You should provide a Minimal Working Example of your code as suggested by Alrubaie. Otherwise, we end up guessing. However, you might want to look at
poly[[1,20000,1]]and see if any points nearly overlap. That is what I meant by degenerate polygons. You could try repairing degenerate polys or ignore them as I did in my answer. – Tim Laska Jun 03 '21 at 19:22 -
Sorry about that. But other than replacing the analytical expression in
ListContourPlot3Dwith some numerical data loaded from a file, the code I tried is exactly the same as the solution you suggested above. The numerical data is quite large so it's not presentable in the post. But I have added an example point which doesn't work withArea. There doesn't seem to be any two points are ''nearly degenerate'', although it is arguable how close is ''nearly degenerate''.. – Dennis Jun 03 '21 at 20:55 -
@Dennis You get an error that
$IterationLimit::itlimis exceeded. If you look at the details section ofPolygon, you see the statementAs a geometric region, the points Subscript[p, i] can have any embedding dimension, but must all lie in a plane and have the same embedding dimension.You will find that the points do not lie in a planeCoplanarPoints[{{10., 22.8529, 4.}, {10.8562, 22., 4.}, {11., 22., 4.34981}, {11., 22.2385, 5.}, {10.2474, 23., 5.}, {10., 23., 4.34491}}]==False. The MWE would help to figure out the easiest way to correct to coplanarity issue. – Tim Laska Jun 03 '21 at 22:03 -
Sorry, I am a newbie to Mathematica. What does MWE refer to? And I wonder if there is a way to get all the triangular mesh of the isosurfaces, which maybe more accurate when sum up the areas and also doesn't have coplanarity issue. – Dennis Jun 03 '21 at 23:31
-
@Dennis MWE = Minimal Working Example. It is hard to troubleshoot your problem without the MWE. You could try adding the option
Mesh -> Allto your plot. When I comment mine out in my answer, the procedure fails. – Tim Laska Jun 04 '21 at 00:12