5

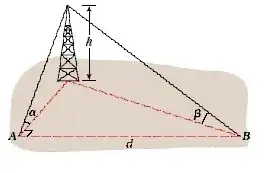
I got a problem of which I can't get mathematica to calculate.

enter image description here

The known inputs are a=17 degree, b=12 degree and side d is 300.

The whole thing is actually 4 right-angled triangles (left side as A, right side as B, the red at bottom as C and the black with the d side as D)

I've tried to type all the equations for the angles and sides I need to get the h value but I can't get a reasonable output.

Remove["Global`*"]
va = 17;
vb = 12;
d = 300;    
Reduce[{(Tan[va]*(Tan[vc]*d)) == (Sin[va]*(Tan[vd]*d)) == (Tan[vb]*(Cos[vc]/d)) == (Sin[vb]*(Cos[vd]/d)), Tan[vc] == (Tan[vc]*d)/d, Cos[vc] == d/(Cos[vc]/d), Tan[vd] == (Tan[vd]*d)/d, Cos[vd] == d/(Cos[vd]/d)}, h] // N

The ouput I get is

Tan[vc] == -0.275163 Tan[vd] && Sec[vd] == 1.79174 Tan[vd] && Sec[vc] == 1.51196 Tan[vd] && Cos[vd] == 161256. Tan[vd] && Cos[vc] == 136077. Tan[vd]

What is it that I'm missing? I can't see how else I should make the equation more elaborate to get allt the sides and angles that is needed to the the value of h.

Johan Grankvist
  • 121
  • 3
  • 1
    I haven't checked your algebra, but you do need to tell Mathematica that your angles are in degrees. It assumes they are radians the way you have written your code. – Bill Watts Jun 03 '21 at 07:24
  • Oh, totally overlooked that. With a small change (forgot to include the variable h) I got an answer but I can't get only that variable as an out put. – Johan Grankvist Jun 03 '21 at 07:30
  • 1
    You claim that there are 4 right-angled triangles. That can not be right. If the red triangle is right-angled, then D, the black triangle, must have an angle smaller than Pi/2. – Daniel Huber Jun 03 '21 at 09:28

2 Answers2

4
va = 17 Degree;
vb = 12 Degree;
d = 300;

Taking x as the length from A to the base of the tower.

Reduce[{
   Tan[va] == h/x,
   Tan[vb] == h/Sqrt[d^2 - x^2]}] // N

x == 171.251 && h == 52.3567

You just need enough expressions to determine your system. If you add too many expressions Mathematica may not find the solution.

Chris Degnen
  • 30,927
  • 2
  • 54
  • 108
1

Updated code. Now the thing is to only get h value as output

va = 17 Degree; vb = 12 Degree; d = 300;
Reduce[{(h == Tan[va]*(Tan[vc]*d)) == (Sin[va]*(Tan[vd]*d)) == (Tan[vb]*
(Cos[vc]/d)) ==(Sin[vb]*(Cos[vd]/d)), Tan[vc] == (Tan[vc]*d)/d, Cos[vc] 
== d/(Cos[vc]/d),Tan[vd] == (Tan[vd]*d)/d, Cos[vd] == d/(Cos[vd]/d)}] 
//N
Johan Grankvist
  • 121
  • 3