How to increase precision: $MinPrecision does not help

Question

I have the following series:

f[x_] := Sin[x]
n := 50

Ni3[x_] := Sum[(f[k]*(-1)^k)/((x - k)*Gamma[k + 1]*Gamma[n - k + 1]), {k, 0, n}]/
           Sum[(-1)^k/((x - k)*Gamma[k + 1]*Gamma[n - k + 1]), {k, 0, n}]

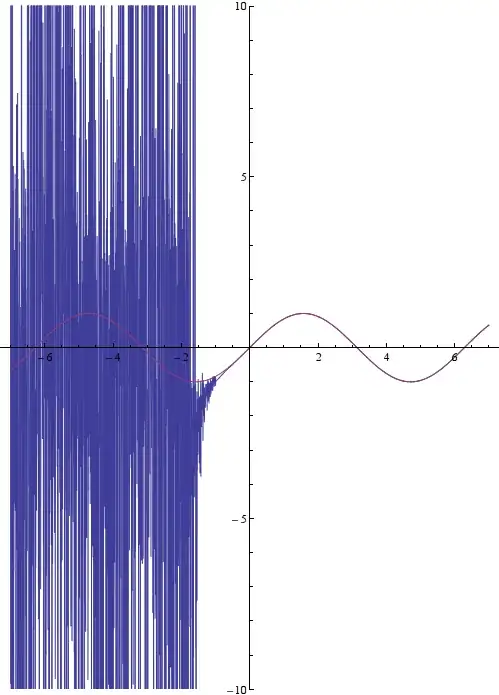
Plot[{Ni3[x], f[x]}, {x, -7, 7}, AspectRatio -> Automatic, PlotRange -> 10]

At number of terms n below 40 the plot gives what is expected. But when increasing it above 50 the plot becomes corrupted. The setting $MinPrecision does not affect the result. The series is proven to converge to $f(x)=\sin(x)$.

bad plot

Try using a high value of WorkingPrecision in Plot, e.g. WorkingPrecision -> 60. — Szabolcs, May 07 '13 at 03:42
@Szabolcs you made incorrect change to the expression, putting one sum inside the other — Anixx, May 07 '13 at 03:44
Sorry about that. When you paste expressions like this, select them, right click, then use Copy As -> Input Form. — Szabolcs, May 07 '13 at 03:47
@Szabolcs I did exactly that. It is what exported as Input Form. — Anixx, May 07 '13 at 03:48

score 4 · Accepted Answer · answered May 07 '13 at 03:49

4

As Szabolcs suggests, cranking up WorkingPrecision (or for that matter, just forcing Plot[] to use arbitrary precision) helps a lot. In this answer, I've taken the liberty to slightly simplify your barycentric interpolant as well:

f[x_] := Sin[x]

Ni3[n_Integer, x_] := (x - n) Binomial[x, n]
    Sum[(-1)^(n - k) Binomial[n, k] f[k]/(x - k), {k, 0, n}, Method -> "Procedural"]

Plot[{Ni3[50, x], f[x]}, {x, -7, 7}, AspectRatio -> Automatic, 
     PlotRange -> 10, WorkingPrecision -> 20]

sine and barycentric interpolant

answered May 07 '13 at 03:49

J. M.'s missing motivation

124,525
11
401
574

How to force it to use arbitrary precision? – Anixx May 07 '13 at 03:50
You get this plot with WorkingPrecision -> 20? I get junk with that ... I needed a much higher value. – Szabolcs May 07 '13 at 03:50
@Szabolcs, well, I simplified OP's function a bit; that helped. – J. M.'s missing motivation May 07 '13 at 03:51
@Anixx, as I said, with WorkingPrecision. – J. M.'s missing motivation May 07 '13 at 03:52
To be precise, it runs out of precision around 1.5 for a precision setting of 20, around -1.2 for 30, and looks fine for 40 (for default plot range). – Szabolcs May 07 '13 at 03:52
@J.M. Ah, I see now. – Szabolcs May 07 '13 at 03:53
@Anixx If you use an explicit WorkingPrecision setting, Mathematica will use its arbitrary precision arithmetic. This doesn't mean that it will use "infinitely many" digits. It'll start with as many digits as you ask for in WorkingPrecision, and it'll try to keep track of how much error accumulates during the calculations. It might run out of precision. Try e.g. your original Ni3 with Ni3[1.1`20]. It'll give you "zero", with a pink background. You can apply Precision to it to verify that it has none. – Szabolcs May 07 '13 at 03:55
@Szabolcs, actually, now that I tried it out, WorkingPrecision -> $MachinePrecision works, too. >:) – J. M.'s missing motivation May 07 '13 at 03:56
@J.M. WorkingPrecision -> MachinePrecision doesn't though. – Szabolcs May 07 '13 at 03:58
What about WorkingPrecision -> $MaxNumber? – Anixx May 07 '13 at 03:58
@Szabolcs, true. That's the cancellation inherent in computing high-degree barycentric interpolants at play. I'm surprised just forcing arbitrary precision and a modest number of digits to work with made for something reasonable. – J. M.'s missing motivation May 07 '13 at 04:01
@Anixx, what for? You could try it out yourself; I won't. – J. M.'s missing motivation May 07 '13 at 04:02
It seems your Lagrange form does not work faster though... – Anixx May 07 '13 at 04:03
@J.M. WorkingPrecision -> $MachinePrecision often works in this situation because switching on significance arithmetic is enough for precision tracking and $MaxExtraPrecision to be able to take care of the rest. – Oleksandr R. May 08 '13 at 11:38
@Oleksandr, I know. ;) – J. M.'s missing motivation May 08 '13 at 11:40

How to increase precision: $MinPrecision does not help

1 Answers1