Using perpendicular offsets in FindFit

Question

I want to use perpendicular offsets in the built-in FindFit function. Are there any possible ways or do I have to code everything by myself?

Answer 1

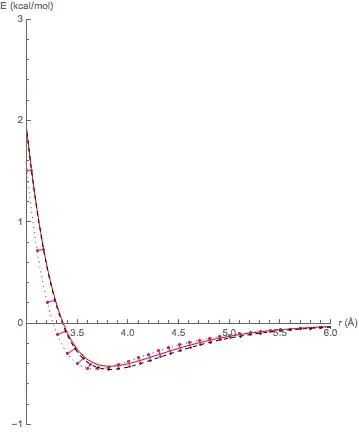
Ok, I had done this long time ago since my supervisor insisted, this is a numerical approach to what you asked for and I have done this for a L-J potential function but can be extended to any function.

I hope this will help you.

In principle we need to minimize the the perpendicular distance. For example if U[r] is our function and E[r] is our energy points (data), we will have to different types of fitting

minimizing U[r]-E[r] =Vertical fit

minimizing U[x]-E[r] =perpendicular fit,

where x is the point on the curve which is perpendicular to our data point.

Problem here is we don't have any coordinates for points on our functional to draw perpendicular lines and minimize them, therefore what I did was doing a normal builtin fitting which would be vertical as an initial guess!

something like:

NMinimize[(U[r] -E[r] ), {A,B,C}]

Then I draw perpendicular lines from the first best vertical fit assumption and minimize them

for that!

you Find Perpendicular coordinates on to the line (here's the x we need!)

FindMinimum[{(E[x] - U[r])^2 + (x - r)^2}, {x,"initial guess"}]

Then minimize this distance by refitting in the same procedure as before but this time instead minimizing E[r]-U[r] you minimize E[r]-U[x] where x is perpendicular to E[r]. after this you can put it in a loop and continue this loop to satisfaction.

[1