How can I mark the maximum value in a plot?

Question

How can I mark the maximum value in a graph?

The graph that I would like to determine its maximum value, is an output of the following program:

im[Δm_, Δa_, c_, κa_, κm_, λ_, ω_] := (
   c κa κa )/(
   4 (κa - (κa λ^2)/(κa^2 + (-Δa - ω)^2))^2 + 
    4 (Δa - ω - (λ^2 (Δa + ω))/(κa^2 + (-Δa - ω)^2))^2) - (
   c κa λ^2 κa)/(
   4 (κa^2 + (-Δa - ω)^2) ((κa - (κa λ^2)/(κa^2 + (-Δa - ω)^2))^2 + (Δa - ω - (λ^2 (Δa + ω))/(κa^2 + (-Δa - ω)^2))^2));
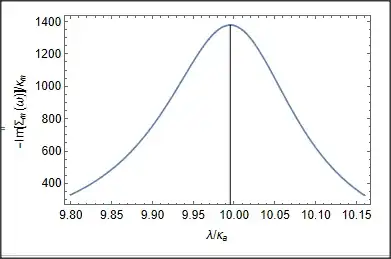
Plot[im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10],
 {x, 0.980 10, 1.016 10}, Frame -> True, 
 FrameLabel -> {"λ/!(*SubscriptBox[(κ), (a)])",
    "-Im[!(*SubscriptBox[(Σ), (m)])(ω)]/!(*SubscriptBox[(κ), (m)])" }, 
 LabelStyle -> Directive[Black, 12], PlotStyle -> Blue]

How can I do it?

Maximize[{im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10], x > 0}, x] — Bob Hanlon, Jun 04 '21 at 07:04

kglr · Answer 1 · 2021-06-04T11:04:33.093

f[x_] := im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10];

1. An alternative way to use MeshFunctions:

Plot[f[x], {x, 0.980 10, 1.016 10}, Frame -> True, 
 FrameLabel -> {"λ/" <> ToString[Subscript[κ, a], StandardForm], 
   "-Im[" <> ToString[Subscript[Σ, m], StandardForm] <> 
    "(ω)]/" <> ToString[Subscript[κ, m], StandardForm]},
 LabelStyle -> Directive[Black, 12], PlotStyle -> Blue, 
 MeshFunctions -> {f'}, 
 Mesh -> {{0}}, 
 MeshStyle -> Directive[Red, PointSize @ Large]]

2. We can also insert the desired primitives using the option DisplayFunction:

displayFunction = Show[#,
  Epilog -> {Red, PointSize @ Large, 
   Point[MaximalBy[Last][Join @@ Cases[Normal@#, Line[x_] :> x, All]]]}] &
Plot[f[x], {x, 0.980 10, 1.016 10}, Frame -> True, 
 PlotStyle -> Blue, 
 DisplayFunction -> displayFunction]

score 7 · Answer 2 · answered Jun 04 '21 at 07:00

You may e.g. use "NMaximize" and "Epilog" like:

pt = NMaximize[{im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 
    0.1 10], 9 < x < 10}, x]
pt = {x, pt[[1]]} /. pt[[2, 1]];
Plot[im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10], {x, 
  0.980 10, 1.016 10}, Frame -> True, 
 FrameLabel -> {"\[Lambda]/\!\(\*SubscriptBox[\(\[Kappa]\), \(a\)]\)",
    "-Im[\!\(\*SubscriptBox[\(\[CapitalSigma]\), \
\(m\)]\)(\[Omega])]/\!\(\*SubscriptBox[\(\[Kappa]\), \(m\)]\)"}, 
 LabelStyle -> Directive[Black, 12], PlotStyle -> Blu, 
 Epilog -> Line[{{pt[[1]], 0}, pt}]]

score 5 · Answer 3 · answered Jun 04 '21 at 07:06

Try this:

fm = FindMaximum[
   im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10], {x, 10}];
coord = {fm[[2, 1, 2]], fm[[1]]};
Show[{
  Plot[im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10], {x, 
    0.980 10, 1.016 10}, Frame -> True, 
   FrameLabel -> {"Text1", "Text2"}, 
   LabelStyle -> Directive[Black, 12], PlotStyle -> Blue],
  Graphics[{Red, PointSize[0.02], Point[coord]}]
  }]

yielding the following plot:

Have fun!

score 3 · Answer 4 · answered Jun 04 '21 at 07:03

You could do it in different ways, one solution is using the Mesh option in the plot:

Use NArgMax to find the maximum value of x and use that value in the mesh to highlight the maximimum point.

Code

Plot[im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 0.1 10], {x, 
  0.980 10, 1.016 10}, Frame -> True, 
 FrameLabel -> {"\[Lambda]/\!\(\*SubscriptBox[\(\[Kappa]\), \(a\)]\)",
    "-Im[\!\(\*SubscriptBox[\(\[CapitalSigma]\), \
\(m\)]\)(\[Omega])]/\!\(\*SubscriptBox[\(\[Kappa]\), \(m\)]\)"}, 
 LabelStyle -> Directive[Black, 12], PlotStyle -> Blue,
Mesh -> {{NArgMax[{im[0.1 10, 1 10, 1000, 0.1 10, 0.000001 10, x, 
       0.1 10], 0.980 10 <= x <= 1.016 10}, x]}}, MeshStyle -> {Red,PointSize[Medium]}]

Result:

How can I mark the maximum value in a plot?

4 Answers4

Code