How to integrate exponential function over implicit function

Question

The following integral can be solved in Mathematica:

Integrate[Exp[a*(z - 1)], {x, y, z}\[Element]Sphere[],Assumptions -> a > 0 && a\[Element]Reals]

Outputs:

But if I change Sphere[] to implicit function, the integral can not be solved:

Integrate[Exp[a*(z - 1)], {x, y, z} \[Element] 
  ImplicitRegion[x^2 + y^2 + z^2 == 1, {x, y, z}], 
 Assumptions -> a > 0 && a \[Element] Reals]

Furthermore, can this integral be solved over a spherical cap?

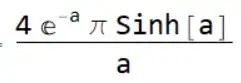
Integrate[Exp[a*(z - 1)], {x, y, z} \[Element] Sphere[], Assumptions -> a <= 0] performs $\frac{4 \pi e^{-a} \sinh (a)}{a}$ too. — user64494, Jun 04 '21 at 14:37

cvgmt · Accepted Answer · 2021-06-04T14:49:29.637

2

I think we need to use ParametricRegion.

reg2 = ParametricRegion[{Cos[θ] Sin[ϕ], 
    Sin[θ] Sin[ϕ], 
    Cos[ϕ]}, {{θ, 0, 2 π}, {ϕ, 0, π/4}}];
Integrate[Exp[a*(z - 1)], {x, y, z} ∈ reg2, 
 Assumptions -> a > 0]
(* Region[reg2, ViewPoint -> {1, 1, -.5}] *)

$$\frac{2 \pi \left(1-e^{\frac{a}{\sqrt{2}}-a}\right)}{a}$$

edited Jun 04 '21 at 14:49

answered Jun 04 '21 at 14:27

cvgmt

72,231
4
75
133

1

Something to adjust: the integrand is positive so does the integral, but $$ \frac{2 \pi \left(1-e^{\frac{a}{\sqrt{2}}-a}\right)}{a}$$ is negative for big $a$. – user64494 Jun 04 '21 at 15:24
1

@user64494, Please note that 1/Sqrt[2] -1< 0 so that the result is positive. – cvgmt Jun 04 '21 at 15:43
1

You are right, I amn't. – user64494 Jun 04 '21 at 16:14

How to integrate exponential function over implicit function

1 Answers1