6

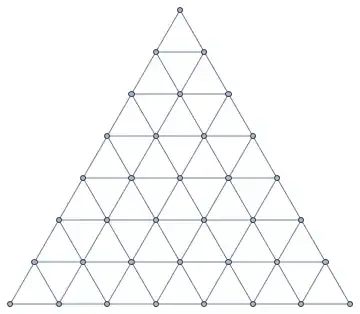
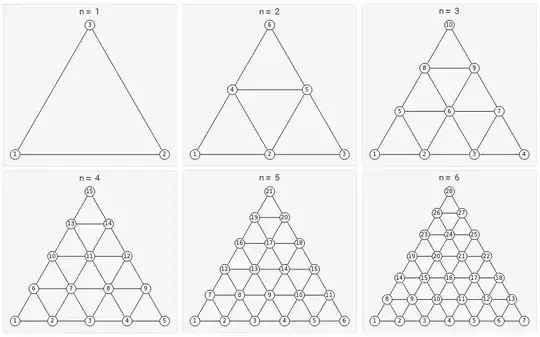
Given a triangular lattice which grows with number n, as follows triangle-lattices

I want to list all the connected points in the lattice to form the pairlist. As an example:

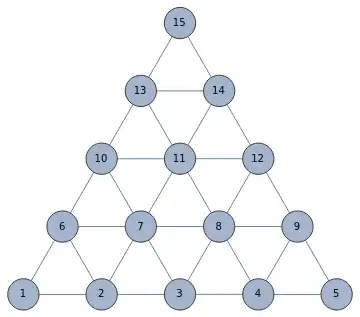
n=1:
pairlist={{p_{1},p_{2}},{p_{1},p_{3}},{p_{2},p_{3}}}
n=2:
pairlist={{p_{1},p_{2}},{p_{1},p_{4}},{p_{2},p_{3}},{p_{2},p_{4}},{p_{2},p_{5}},{p_{3},p_{5}},{p_{4},p_{5}},{p_{4},p_{6}},{p_{5},p_{6}}}
n=3:
pairlist={{p_{1},p_{2}},{p_{1},p_{5}},{p_{2},p_{3}},{p_{2},p_{5}},{p_{2},p_{6}},{p_{3},p_{4}},{p_{3},p_{6}},{p_{3},p_{7}},{p_{4},p_{7}},{p_{5},p_{8}},{p_{5},p_{6}},{p_{6},p_{8}},{p_{6},p_{9}},{p_{6},p_{7}},{p_{7},p_{9}},{p_{8},p_{10}},{p_{8},p_{9}},{p_{9},p_{10}}}

Notice that there is no need to list the elements in pairlist in order.

Questions:

  1. Is there some automatical way to do above tasks?
  2. If I have points= Flatten[Table[Subscript[p, i], {i, 1, Binomial[n + 2, 2]}]];, how can I create the triangle lattice with points automatically?

For Question-2, I make one code for n=2 in the below (is there any simple and general way for different n?).

pairlists = {};
n = 2;
points = Flatten[Table[Subscript[p, i], {i, 1, Binomial[n + 2, 2]}]];

For[ii = 1, ii <= Length[points], ii++,
 For[jj = ii + 1, jj <= Length[points], jj++,


If[(Abs[points[[ii]][[2]]-points[[jj]][[2]]]==1&&ii != 3) ||(Abs[points[[ii]][[2]]-points[[jj]][[2]]]==2&&Abs[ii-jj]==2&& ii!=1 )||(Abs[points[[ii]][[2]]-points[[jj]][[2]]]==3&&Abs[ii-jj]==3&&ii!=3),


  AppendTo[pairlists, {points[[ii]], points[[jj]]}];
]



];
 ]
Xuemei
  • 1,616
  • 6
  • 10

2 Answers2

6
basis = {{1, 0}, {Cos[60 Degree], Sin[60 Degree]}};
genpts[n_] :=
 # . basis & /@
  Select[
   Flatten[CoordinateBoundsArray[{{0, n}, {0, n}}], 1],
   Total[#] < n &
  ]

g = With[{pts = genpts[8]}, 
  NearestNeighborGraph[pts, VertexCoordinates -> pts]]

triangular lattice

You can then get pairs of connected vertices as follows:

EdgeList[g] /. UndirectedEdge -> List
flinty
  • 25,147
  • 2
  • 20
  • 86
  • nice, thank you! What if I don't have the lattice at the begin but I have points with labels p_{i}, how can I automatically get the triangular lattice pattern? – Xuemei Jun 10 '21 at 12:04
  • p_{i} isn't Mathematica syntax. You can just do g = NearestNeighborGraph[points, VertexCoordinates -> points] where points is a list of the coordinates. No need for labels / symbols here. – flinty Jun 10 '21 at 12:06
  • Sorry, p_{i} is just Subscript[p,i]. I don't know how to write in the stackexchange. – Xuemei Jun 10 '21 at 12:07
  • actually, I need to make labels/symbols. Because later I want to use the symbols for some defined function such as f[expr,p1,p2]=expr*(1+p1*p2), which are not values. @flinty – Xuemei Jun 10 '21 at 12:20
  • I add one example for n=2 for question 2, could you also have a look? Thank you very much! – Xuemei Jun 10 '21 at 13:09
  • Don't do that with symbols etc. do points[[1]], points[[2]] instead of p1,p2. – flinty Jun 10 '21 at 13:24
4
 triangleGridGraph[n_, opts : OptionsPattern[]] := 
  Module[{vc = Join @@ Table[{j + i/2, i Sqrt[3]/2}, {i, 0, n + 1}, {j, 0,  n - i}]},
    NearestNeighborGraph[vc, VertexCoordinates -> vc, opts]]

Examples:

triangleGridGraph[4, 
  VertexLabels -> Placed["Index", Center], VertexSize -> Large]

enter image description here

IndexGraph[triangleGridGraph[4], 
  VertexLabels -> {v_:> Placed[Subscript[P, v], Center]},
  VertexSize->Large]

enter image description here

Multicolumn[Panel[
  Labeled[
    triangleGridGraph[#, GraphStyle -> "IndexLabeled", ImageSize -> 300], 
    Style[PromptForm["n", #], 16], Top]] & /@ Range[6], 
  3, Appearance -> "Horizontal"]

enter image description here

To get edges as lists, you Apply List at level 1 to EdgeList of triangleGridGraph[n]. For example,

List @@@ EdgeList[triangleGridGraph[2]]

{{{0, 0}, {1, 0}}, {{0, 0}, {1/2, Sqrt[3]/2}}, {{1, 0}, {2, 0}}, 
 {{1, 0}, {1/2, Sqrt[3]/2}}, {{1, 0}, {3/2, Sqrt[3]/2}}, 
 {{2, 0}, {3/2, Sqrt[3]/2}}, {{1/2, Sqrt[3]/2}, {3/2, Sqrt[3]/2}},  
 {{1/2, Sqrt[3]/2}, {1, Sqrt[3]}}, {{3/2, Sqrt[3]/2}, {1, Sqrt[3]}}}
kglr
  • 394,356
  • 18
  • 477
  • 896