Getting dihedrals of a polyhedron object

Question

I am generating a refined icosahedron as follows:

Needs["PolyhedronOperations`"]
Geodesate[PolyhedronData["Icosahedron"], 3]

The output is:

I can also exract the face coordinates as

faces = Cases[Normal@Geodesate[PolyhedronData["Icosahedron"], 3], _Polygon, Infinity];
f = faces // N;

My question is, how to get all the dihedral angle values between all neighboring faces? I'm using Mathematica 11.3.0.0 and neither the functions DihedralAngle nor PolyhedronAngle seem to be implemented.

Welcome to Mathematica.SE! I hope you will become a regular contributor. To get started, 1) take the introductory [tour] now, 2) when you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge, 3) remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign, and 4) give help too, by answering questions in your areas of expertise. — bbgodfrey, Jun 16 '21 at 17:35

Craig Carter · Accepted Answer · 2021-06-16T18:56:49.393

I am afraid that one has to resort to extracting the geometry. Here is an example:

Needs["PolyhedronOperations`"]
hedron = Geodesate[PolyhedronData["Icosahedron"], 3]

Extract points.

pts = Cases[hedron, GraphicsComplex[pts_, other__] :> pts][[1]]

Extract indices of polygons

polygons = 
 Cases[hedron, GraphicsComplex[pts_, Polygon[other_]] :> other][[1]]

Write a function to give the normal to the polygon from its points and indices.

normal[pts_, indices_] := 
 With[{a = pts[[indices[[2]]]] - pts[[indices[[1]]]], 
   b = pts[[indices[[3]]]] - pts[[indices[[2]]]]},
  Simplify[Normalize[Cross[a, b]]]
  ]

Compute the normals for each facet (I made this numerical, otherwise the expressions become very long)

normals = normal[N@pts, #] & /@ polygons

Create a handy set of associations for each polygon

polygonAssocs = 
 MapThread[<|"polygon" -> #1, 
    "edges" -> Transpose[{#2, RotateLeft[#2]}], 
    "normal" -> #3 |> &, {Range[Length[polygons]], polygons, normals}]

e.g.

RandomChoice[polygonAssocs]

Make a list of all edges on the polygons, keep only the ordered ones.

allEdges = 
 Select[Flatten[polygonAssocs[[All, "edges"]] , 1], OrderedQ]

A function to see if a polygon contains an edge, either ordered or not. Arrange the pair so that the first polygon is the one containing the oriented edge.

containsEdge[pgonAssoc_, edge : {e1_, e2_}] :=
   With[{polygons = 
    Select[pgonAssoc, MemberQ[#edges, {e1, e2} | {e2, e1}] &]},
  Which[
   MemberQ[polygons[[1, "edges"]], edge], polygons,
   True, Reverse[polygons]
   ]
  ]

For each edge, find the neighboring polygons, and compute the dot-product of their normals.

edgePolygons =
 MapThread[
  With[
    {edge = #1, polygonPair = containsEdge[polygonAssocs, #2]},
    <|"edge" -> edge, "polygons" -> polygonPair, 
     "dihedral" -> 
      ArcCos[
       First[polygonPair]["normal"] . Last[polygonPair]["normal"]]
     |>] &, {Range[Length[allEdges]], allEdges}]

e.g.,

RandomChoice[edgePolygons]

thank you for your detailed answer; I must confess though I'm struggling with understanding it. Could be a version mismatch, but I'm getting an error from MapThread: MapThread::mptd: Object normals at position {2, 3} in MapThread[Association[polygon->#1,edges->Transpose[{#2,RotateLeft[Slot[<<1>>]]}],normal->#3]&, ... has only 0 of required 1 dimensions — Botond, Jun 16 '21 at 18:36
Oh, I forgot to copy and paste the line that computes the normals. It is now edited. If you are having difficulty understand bits of the code, don't hesitate to ask. I can add more verbage. — Craig Carter, Jun 16 '21 at 18:57
thank you, @Craig Carter. I'm still digesting all the details, but tested it, runs and works and gives the correct result. — Botond, Jun 16 '21 at 19:43

kglr · Answer 2 · 2021-06-17T18:35:39.393

Update: A more direct approach using Region`Mesh`MeshCellNormals and "EdgeFaceConnectivity" to get a Dataset with "edge" (edge index) "faces" (indices of faces connected to "edge"), "facenormals" (normal vectors for "faces"), and "dihedral" (dihedral angle of "faces") as columns:

ClearAll[edgeDihedrals]
edgeDihedrals[bmr_] := Module[{fn = Region`Mesh`MeshCellNormals[bmr, 2]}, 
 Dataset @ MapIndexed[Association @ {"edge" -> #2[[1]], "faces" -> #, 
   "facenormals" -> AssociationThread[#, fn[[#]]], 
   "dihedral" -> ArcCos[Dot @@ fn[[#]]]} &] @ bmr["EdgeFaceConnectivity"]]

Examples:

bdg = BoundaryDiscretizeGraphics @  Geodesate[PolyhedronData["Icosahedron"], 3];
edgeDihedrals[bdg]

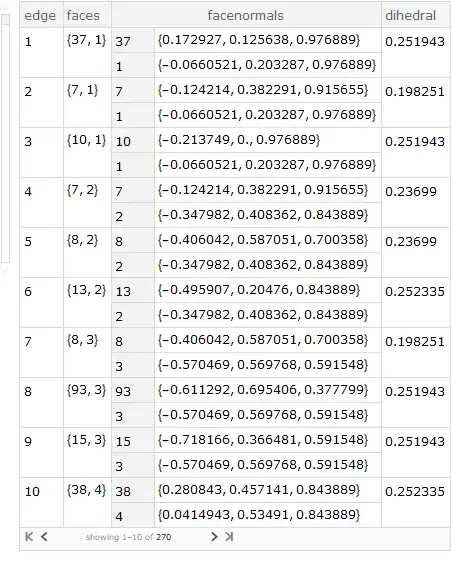
edgeDihedrals[bdg][Range[10], {"edge", "faces", "dihedral"}]

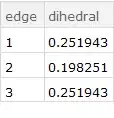
edgeDihedrals[bdg][{1, 2, 3}, {"edge", "dihedral"}]

HighlightMesh[bdg, 
  {Style[{1, 1}, Thick, Red], 
   ## & @@ Thread[{2, Normal @ edgeDihedrals[bdg][1, "faces"]}], 
   Style[{1, 15}, Thick, Green], 
   ## & @@ Thread[{2, Normal @ edgeDihedrals[bdg][15, "faces"]}]}, 
 PlotTheme -> "FaceNormals"]

edgeDihedrals @ BoundaryDiscretizeGraphics @ PolyhedronData["Tetrahedron"]

Original answer:

First, use BoundaryDiscretizeGraphics to get a BoundaryMeshRegion object:

bdg = BoundaryDiscretizeGraphics @  Geodesate[PolyhedronData["Icosahedron"], 3];

We can identify faces connected thru an edge using the properties "FaceVertexConnectivity" and "FaceFaceConnectivity". Then, we can use the function Region`Mesh`MeshCellNormals to get normals for each pair of neighboring faces and use Dot + ArcCos to get the dihedral angles.

ClearAll[neighboringFaces, dihedralAngle]
neighboringFaces[bmr_] := Module[{faces = bmr["FaceVertexConnectivity"]}, 
   Association @ MapIndexed[Function[{x, ind}, ind[[1]] -> 
     DeleteCases[x, _?(Length[Intersection[faces[[ind[[1]]]], faces[[#]]]] != 2 &)]], 
    bmr["FaceFaceConnectivity"]]];
dihedralAngle[bmr_][i_, j_] /; MemberQ[neighboringFaces[bmr][i], j] :=
    ArcCos[Dot @@ RegionMeshMeshCellNormals[bmr, {{2, i}, {2, j}}]]

Examples:

neighboringFaces[bdg][1]

 {7, 10, 37}

neighboringFaces[bdg][15]

 {3, 18, 100}

HighlightMesh[bdg, {Style[{2, 1}, Red], ## & @@ Thread[{2, neighboringFaces[bdg][1]}], 
  Style[{2, 15}, Green], ## & @@ Thread[{2, neighboringFaces[bdg][15]}]}, 
 PlotTheme -> "FaceNormals"]

{1, #} -> dihedralAngle[bdg][1, #] & /@ neighboringFaces[bdg][1]

 {{1, 7} -> 0.198251, {1, 10} -> 0.251943, {1, 37} -> 0.251943}

{15, #} -> dihedralAngle[bdg][15, #] & /@ neighboringFaces[bdg][15]

 {{15, 3} -> 0.251943, {15, 18} -> 0.198251, {15, 100} -> 0.251943}

$Version

"11.3.0 for Microsoft Windows (64-bit) (March 7, 2018)"

Getting dihedrals of a polyhedron object

2 Answers2