Plotting Lines of Intersection of Two Surface

Question

ContourPlot3D[{(2 + a \[Gamma])^2/(2 (-4 + \[Gamma]^2)^2) ==
-(((-1 + r) (-8 + (3 + r) \[Gamma]^2 + a \[Gamma] (-6 + (2 + r) \[Gamma]^2))^2)/(4 (-2 + \[Gamma]^2)^2 (-4 + (1 + r) \[Gamma]^2)^2)), 
(-2 + a (-1 + r) \[Gamma] + r \[Gamma]^2)^2/(4 (-2 + \[Gamma]^2) (-4 + (1 + r) \[Gamma]^2)) == 
-(((-1 + r) (2 + a \[Gamma])^2)/(-4 + \[Gamma]^2)^2)}, 
{\[Gamma], 0, 1}, {a, 0, 1}, {r, 0.4, 1}, PlotLegends -> Automatic]

Knowing the two surface equations in three-dimensional space, how can we quickly draw the intersection line.

Since the two surface equations are relatively complicated, if r is solved, multiple roots will be obtained. At this time, it is also necessary to determine which root is available, so it will be more complicated.

Therefore, I hope to find a faster drawing method.

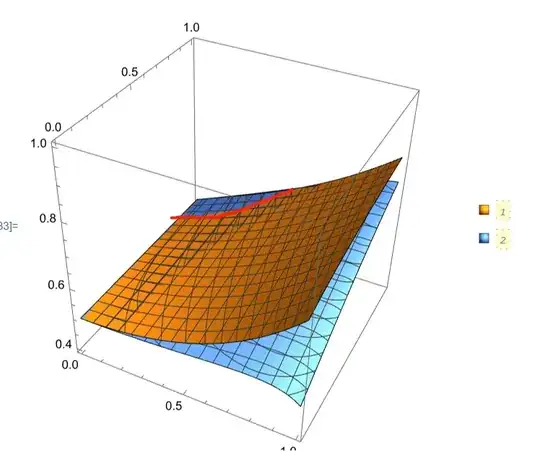
Possible duplicate: https://mathematica.stackexchange.com/questions/5968/plotting-implicitly-defined-space-curves — add the option BoundaryStyle -> {{1, 2} -> Directive[Red, Thick]} — Michael E2, Jun 18 '21 at 18:02

cvgmt · Answer 1 · 2021-06-19T08:34:35.833

One way is as below.

reg1 = ImplicitRegion[(2 + 
        a γ)^2/(2 (-4 + γ^2)^2) == -(((-1 + 
           r) (-8 + (3 + r) γ^2 + 
            a γ (-6 + (2 + 
                  r) γ^2))^2)/(4 (-2 + γ^2)^2 (-4 + (1 +
                r) γ^2)^2)), {{γ, 0, 1}, {a, 0, 1}, {r, 
     0.4, 1}}];
reg2 = ImplicitRegion[(-2 + a (-1 + r) γ + 
        r γ^2)^2/(4 (-2 + γ^2) (-4 + (1 + 
            r) γ^2)) == -(((-1 + 
           r) (2 + a γ)^2)/(-4 + γ^2)^2), {{γ, 0,
      1}, {a, 0, 1}, {r, 0.4, 1}}];
reg3 = RegionIntersection[reg1, reg2];
Show[DiscretizeRegion[reg3, BaseStyle -> {Thick, Red}, 
  MaxCellMeasure -> 10^-6], 
 DiscretizeRegion[reg1, BaseStyle -> Yellow, MaxCellMeasure -> 10^-6],
  DiscretizeRegion[reg2, BaseStyle -> Cyan, MaxCellMeasure -> 10^-6]]