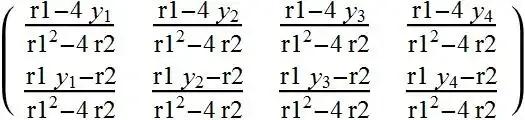How to find and apply variable substitutions that simplify an expression?

Question

I have a simple matrix expression.

A = ( {
    {Subscript[y, 1], 1},
    {Subscript[y, 2], 1},
    {Subscript[y, 3], 1},
    {Subscript[y, 4], 1}
   } );
result = Inverse[Transpose[A] . A] . Transpose[A]

When you run this command, you see the following matrix result:

Clearly, it's quite large, but could be massively simplified with a change of variables or two. Such as:

r2 = y_1^2+y_2^2+y_3^2+y_4^2
r1 = y_1  + y_2 +y_3  +y_4

Inspired by this question: How to simplify an expression, using a known term substitution?, I tried using simplify a few different ways that just didn't work:

Simplify[result, 
 b == Subscript[y, 1] + Subscript[y, 2] + Subscript[y, 3] + Subscript[ y, 4]]

The problem appears to be that Simplify first simplifies the partial fractions, and that leads it down paths where my "simple" substitution becomes difficult/complicated for it to see. Is there a way to have Mathematica rewrite this expression in terms of the individual y's and r1 and r2?

Possible duplicate: https://mathematica.stackexchange.com/questions/181818/finding-sub-expressions-that-simplify-larger-formula/182061 — Szabolcs, Jun 19 '21 at 07:48
Thank you @Szabolcs, that is a very helpful question/answer. — John, Jun 20 '21 at 14:43

Akku14 · Answer 1 · 2021-11-16T09:10:33.747

Also Simplify can do the job, if you feed appropriate TransformationFunctions

{g1[-Subscript[y, 1] - Subscript[y, 2] - Subscript[y, 3] - Subscript[y, 4]] := -r1, 
 g2[Subscript[y, 1] + Subscript[y, 2] + Subscript[y, 3] + Subscript[y, 4]] := r1, 
 g3[Subscript[y, 1]^2 + Subscript[y, 2]^2 + Subscript[y, 3]^2 + Subscript[y, 4]^2] := r2};
Simplify[result, TransformationFunctions -> {g1, g2, g3}] // 
  Simplify // TraditionalForm

score 1 · Accepted Answer · answered Jun 18 '21 at 22:12

1

I recommend that you avoid using subscripts except for display. Use indexed variables formatted as subscripts.

Clear["Global`*"]
Format[y[n_]] = Subscript[y, n];
Format[r[n_]] = Subscript[r, n];
A = {{y[1], 1}, {y[2], 1}, {y[3], 1}, {y[4], 1}};
(result = 
    Inverse[Transpose[A] . A] . Transpose[A] /. {Total[Array[y, 4]] :> r[1],
       Total[-Array[y, 4]] :> -r[1],
       Total[Array[y[#]^2 &, 4]] :> r[2]} // Simplify) // 
  TraditionalForm // MatrixForm

Note that the wrappers (TraditionalForm and MatrixForm) used for display are isolated from the definition of result by the use of parentheses.

answered Jun 18 '21 at 22:12

Bob Hanlon

157,611
7
77
198

Ah, that is very sweet syntax! Thank you! That is incredibly helpful for future work. My comment to Alexi's solution applies to this one as well. – John Jun 19 '21 at 02:48
And for what it's worth, the subscripts question was one I had, but didn't know how to ask. Thanks! That is just huge. – John Jun 19 '21 at 03:04

score 0 · Answer 3 · answered Jun 18 '21 at 20:54

0

Try this:

(result /. \!\(
\*SubsuperscriptBox[\(y\), \(1\), \(2\)] + 
\*SubsuperscriptBox[\(y\), \(2\), \(2\)] + 
\*SubsuperscriptBox[\(y\), \(3\), \(2\)] + 
\*SubsuperscriptBox[\(y\), \(4\), \(2\)]\) -> r1 /. 
    Subscript[y, 1] + Subscript[y, 2] + Subscript[y, 3] + Subscript[y,
       4] -> r2 /. -Subscript[y, 1] - Subscript[y, 2] - Subscript[y, 
     3] - Subscript[y, 4] -> -r2) // Simplify
(*  {{(r2 - 4 Subscript[y, 1])/(-4 r1 + r2^2), (
  r2 - 4 Subscript[y, 2])/(-4 r1 + r2^2), (
  r2 - 4 Subscript[y, 3])/(-4 r1 + r2^2), (
  r2 - 4 Subscript[y, 4])/(-4 r1 + r2^2)}, {(
  r1 - r2 Subscript[y, 1])/(4 r1 - r2^2), (r1 - r2 Subscript[y, 2])/(
  4 r1 - r2^2), (r1 - r2 Subscript[y, 3])/(4 r1 - r2^2), (
  r1 - r2 Subscript[y, 4])/(4 r1 - r2^2)}} *)

Have fun!

answered Jun 18 '21 at 20:54

Alexei Boulbitch

39,397
2
47
96

So, it's disappointing to me, that one has to force the + and - versions of the rules. i.e. that means this approach is extremely fragile, and any variations of my question will require alternative approaches to address. I don't see a way around this, I just bring it up in case you do. – John Jun 18 '21 at 21:30
@John It depends on the problem you are facing. In general, usually one can try to find a more compact way to do that, if it is worth doing. In my view, if I do the analytical calculation the best way is the fastest one, rather than a universal one. What can be faster than copy-pasting two-three expressions from your formula? Another story could be if your expression were more complex. Then thinking of a more universal rule pays off. – Alexei Boulbitch Jun 19 '21 at 10:27

How to find and apply variable substitutions that simplify an expression?

3 Answers3