Make matrixes with numbered name

Question

Suppose I have two matrixes

 M1 = {{0, 0}, {0, 0}}
 M2 = {{0, 0}, {0, 0}}

Now I wanna have $N$ matrixes in this form called M1, M2, M3, M4,...MN

How to code to make $N$ matrixes with the name Mn?

I would like to avoid using an indexed variable approach

May I ask about the reasons for your requirement of " avoid using an indexed variable approach". What about working with rank-3 tensors? — yarchik, Jun 20 '21 at 17:58
Is there anything you can do with named variables that you can't do with the rank-3 approach? — mikado, Jun 20 '21 at 21:13
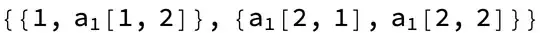
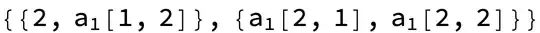
There is also Table["M" <> IntegerString[i, 10, 2], {i, 1, 16}], giving {M01, M02, M03, M04, M05, M06, M07, M08, M09, M10, M11, M12, M13, M14, M15, M16}, or (if you prefer hexadecimal!) Table["M" <> IntegerString[i, 16, 2], {i, 1, 16}] giving {M01, M02, M03, M04, M05, M06, M07, M08, M09, M0a, M0b, M0c, M0d, M0e, M0f, M10} or maybe on a scale of 1 to 10 Table["M" <> IntegerString[i, 2, 8], {i, 1, 10}] giving {M00000001, M00000010, M00000011, M00000100, M00000101, M00000110, M00000111, M00001000, M00001001, M00001010} :-) — user1066, Jun 21 '21 at 08:23

score 7 · Accepted Answer · answered Jun 20 '21 at 17:38

You can use ToString and ToExpression to form the variable names and make assignments to them.

Variable names:

varNames = Table["M" <> ToString[i], {i, 12}]
(* {"M1", "M2", "M3", "M4", "M5", "M6", "M7", "M8", "M9", "M10", "M11", "M12"} *)

Clear variables:

Clear /@ varNames;

Assign matrices:

Do[Evaluate[ToExpression[m]] = RandomReal[10, {2, 2}], {m, varNames}]

Get a matrix:

M3
(* {{7.16959, 8.2422}, {6.35256, 9.84186}} *)

Get another matrix:

M10
(* {{7.0324, 7.755}, {0.0542816, 4.98438}} *)
```

Bob Hanlon · Answer 2 · 2021-06-20T16:34:38.147

4

$Version

(* "12.3.0 for Mac OS X x86 (64-bit) (May 10, 2021)" *)

Clear["Global`*"];

Use an indexed variable m[n] rather than mn

Format[a[n_]] := Subscript[a, n]
m[n_Integer?Positive] := Array[a[n][##] &, {2, 2}]
Column[MatrixForm[m[#]] & /@ Range[3]]

m[20] // MatrixForm

EDIT: Re your comment below, since a1 is not a matrix. a[1][[1, 1]] is not the correct syntax. Use

a[1][1, 1] = 1;

then when m[1] is generated

m[1]

Since m[1] is a matrix, to replace m[1][[1,1]]

ReplacePart[m[1], {1, 1} -> 2]

Or first store m[1]

mat = m[1]

and make a replacement in the stored copy

mat[[1, 1]] = 2;
mat

edited Jun 20 '21 at 16:34

answered Jun 20 '21 at 15:24

Bob Hanlon

Thanks! Using indexed variable approach, how to avoid assignment problems? For example a[1][[1, 1]] = 1 gives the error Set::setps: Subscript[a, 1] in the part assignment is not a symbol. – Nigel1 Jun 20 '21 at 15:59
1

@Nigel1 See this question for some approaches on how to deal with that – Lukas Lang Jun 21 '21 at 08:14

mikado · Answer 3 · 2021-06-20T21:11:59.253

2

There are of course many ways to do this, but often the approach of creating a 3D array is the most systematic

M1 = {{0, 0}, {0, 0}};
M2 = {{0, 0}, {0, 0}};
M = {M1, M2};

You can access whole arrays

M[[2]]
(* {{0, 0}, {0, 0}} *)

and update individual elements

M[[1]][[2, 2]] = 7;
M[[1]]
(* {{0, 0}, {0, 7}} *)

edited Jun 20 '21 at 21:11

answered Jun 20 '21 at 19:08

mikado

3 Answers3