Fill (shade) under a ListLinePlot curve between two abscissae (abscissas?)

Question

I need to fill (shade) between a curve of a ListLinePlot and the axis. The goal is to show students a representation of a definite integral as the area under the curve between two abscissae (abscissas?).

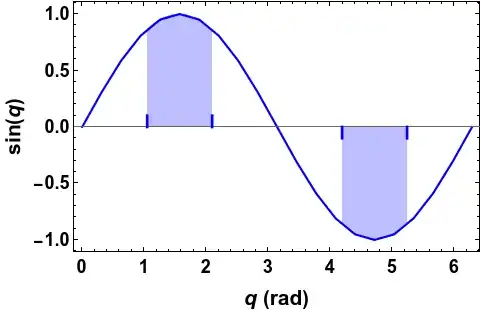
In the example below, list is a set of points representing Sin[q], q being an angle. I would like to fill (shade) between the curve and the axis, for q = Pi / 3 to 2 Pi / 3, and from q = 4 Pi / 3 to 5 Pi / 3 (as shown by the vertical hash marks). Can one do this using Filling?

list = Table[{q, Sin[q]}, {q, 0, 2 Pi, Pi/10}];
Show[{
  ListLinePlot[list, PlotRange -> All, Frame -> True, 
   FrameLabel -> {"q (rad)", "sin(q)"}, PlotStyle -> Blue],
  ParametricPlot[{{Pi/3, u}, {2 Pi/3, u}}, {u, 0, 0.1}, 
   PlotRange -> All, PlotStyle -> Blue],
  ParametricPlot[{{4 Pi/3, u}, {5 Pi/3, u}}, {u, -0.1, 0}, 
   PlotRange -> All, PlotStyle -> Blue]
  }]

Have you seen this? The trick is to use linear interpolation f = Interpolation[list, InterpolationOrder -> 1] and then apply the methods in the linked question to that function. — J. M.'s missing motivation, Jun 30 '21 at 19:45

score 1 · Answer 1 · answered Jun 30 '21 at 20:01

There are a lot of good answers in the link from @J. M. torpor, but here's a very naive solution

Show[{ListLinePlot[list, PlotRange -> All, Frame -> True, 
   FrameLabel -> (Style[#, Black, Bold, 16] & /@ {ToString[q,TraditionalForm] <> " (rad)", 
       ToString[Sin@q, TraditionalForm]}), PlotStyle -> Blue, FrameStyle -> Directive[Black, Bold, 14], 
   Epilog -> {Thick, Blue, Table[Line[{{x, 0}, {x, (-1)^Boole[x > \[Pi]] 0.1}}], {x, {Pi/3, 2 Pi/3, 4 Pi/3, 5 Pi/3}}]}],
  Plot[Sin[q], {q, Pi/3, 2 Pi/3}, PlotRange -> {-1, 1}, PlotStyle -> Opacity[0], Filling -> {1 -> {Axis, Directive[Opacity[0.25], Blue]}}],
  Plot[Sin[q], {q, 4 Pi/3, 5 Pi/3}, PlotRange -> {-1, 1}, PlotStyle -> Opacity[0], Filling -> {1 -> {Axis, Directive[Opacity[0.25], Blue]}}]}]

Basically just add 2 new plots with the bounds you want and fill those. This gives

Fill (shade) under a ListLinePlot curve between two abscissae (abscissas?)

1 Answers1