How can I make a region for boundary conditions for a 3D geometry?

Question

I sometimes work with pipes which can take up complicated positions in 3D geometries. Here is a minimum working example of what I am trying to do.

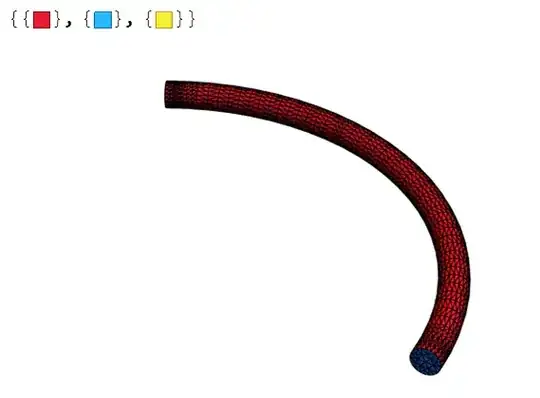
Suppose I want to mesh and calculate vibration frequencies for this solid curved tube.

R0 = 1;
r = 0.05;
ϕ = 0.654 π;
g = Graphics3D[{CapForm["Butt"],
   Tube[Table[{R0 Cos[θ], R0 Sin[θ], 0}, {θ,
      0, ϕ, ϕ/25}], r]}, Axes -> True,
  AxesLabel -> {"x", "y", "z"}]

I can make a mesh for my tube easily:

Needs["NDSolve`FEM`"];
reg = BoundaryDiscretizeGraphics[g,
      MaxCellMeasure -> {"Area" -> 0.001} ]

Now I need a stress operator and boundary conditions. I give the stress operator below and add boundary conditions on one end of the tube which is easy. However, on the other end of the tube I also want to add boundary conditions which is difficult and the reason for my question. To get going I don't add boundary conditions on the "difficult" end.

ClearAll[stressOperator, u, v, w, x, y, z, Y, ν];
stressOperator[
  Y_, ν_] := {Inactive[
     Div][{{0, 0, -((Y*ν)/((1 - 2*ν)*(1 + ν)))}, {0, 0,
       0}, {-Y/(2*(1 + ν)), 0, 0}} .
     Inactive[Grad][w[x, y, z], {x, y, z}], {x, y, z}] +
   Inactive[
     Div][{{0, -((Y*ν)/((1 - 2*ν)*(1 + ν))),
       0}, {-Y/(2*(1 + ν)), 0, 0}, {0, 0, 0}} .
     Inactive[Grad][v[x, y, z], {x, y, z}], {x, y, z}] +
   Inactive[
     Div][{{-((Y*(1 - ν))/((1 - 2*ν)*(1 + ν))), 0,
       0}, {0, -Y/(2*(1 + ν)), 0}, {0, 0, -Y/(2*(1 + ν))}} .
     Inactive[Grad][u[x, y, z], {x, y, z}], {x, y, z}],
  Inactive[Div][{{0, 0, 0}, {0,
       0, -((Y*ν)/((1 -
              2*ν)*(1 + ν)))}, {0, -Y/(2*(1 + ν)), 0}} .
     Inactive[Grad][w[x, y, z], {x, y, z}], {x, y, z}] +
   Inactive[
     Div][{{0, -Y/(2*(1 + ν)),
       0}, {-((Y*ν)/((1 - 2*ν)*(1 + ν))), 0, 0}, {0, 0,
       0}} . Inactive[Grad][u[x, y, z], {x, y, z}], {x, y, z}] +
   Inactive[
     Div][{{-Y/(2*(1 + ν)), 0,
       0}, {0, -((Y*(1 - ν))/((1 - 2*ν)*(1 + ν))), 0}, {0,
        0, -Y/(2*(1 + ν))}} .
     Inactive[Grad][v[x, y, z], {x, y, z}], {x, y, z}],
  Inactive[Div][{{0, 0, 0}, {0,
       0, -Y/(2*(1 + ν))}, {0, -((Y*ν)/((1 -
              2*ν)*(1 + ν))), 0}} .
     Inactive[Grad][v[x, y, z], {x, y, z}], {x, y, z}] +
   Inactive[
     Div][{{0, 0, -Y/(2*(1 + ν))}, {0, 0,
       0}, {-((Y*ν)/((1 - 2*ν)*(1 + ν))), 0, 0}} .
     Inactive[Grad][u[x, y, z], {x, y, z}], {x, y, z}] +
   Inactive[
     Div][{{-Y/(2*(1 + ν)), 0, 0}, {0, -Y/(2*(1 + ν)), 0}, {0,
        0, -((Y*(1 - ν))/((1 - 2*ν)*(1 + ν)))}} .
     Inactive[Grad][w[x, y, z], {x, y, z}], {x, y, z}]};

Here is the code for the boundary conditions on the easy end;

{vals, funs} = NDEigensystem[{stressOperator[10^3, 33/100],
    DirichletCondition[u[x, y, z] == 0,
     y == 0 && (x - R0)^2 + z^2 <= r^2],
    DirichletCondition[v[x, y, z] == 0,
     y == 0 && (x - R0)^2 + z^2 <= r^2],
    DirichletCondition[w[x, y, z] == 0,
     y == 0 && (x - R0)^2 + z^2 <= r^2]},
   {u, v, w}, {x, y, z} \[Element] mesh, 12];

Here are the vibration frequencies:

TableForm[Sqrt[vals], TableHeadings -> {Automatic, None}]

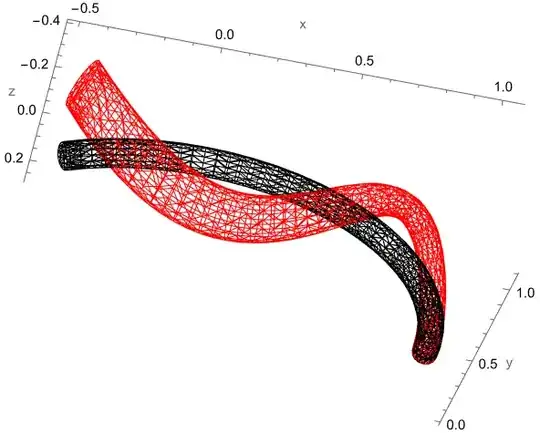
This is an example of a deflected vibration eigenmode:

n = 6;
fac = 0.02;
uif = funs[[n, 1]];
vif = funs[[n, 2]];
wif = funs[[n, 3]];
dmesh = ElementMeshDeformation[mesh, {uif, vif, wif},
   "ScalingFactor" -> fac];
Show[mesh["Wireframe"],
 dmesh["Wireframe"[
   "ElementMeshDirective" -> Directive[EdgeForm[Red], FaceForm[]]]],
 Axes -> True, AxesLabel -> {"x", "y", "z"}]

So everything seems to be working and the issue is: How do I add a DirichletCondition boundary condition on the difficult end? I have to be able to specify the region. My first thought was to identify nodes, making the end region I wish to specify, and then make a MeshRegion. This is not straightforward, particularly in the general case, because you have to define a region to select the coordinates. So the most general question would be: How do you define a region of a mesh where you wish to add a boundary condition?

score 9 · Accepted Answer · answered Jul 07 '21 at 13:34

If you increase the resolution of your BoundaryDiscretizeGraphics, BoundaryElementMarkerUnion will separate your shape into three nice features as shown below.

Needs["NDSolve`FEM`"];
reg = BoundaryDiscretizeGraphics[g, 
   MaxCellMeasure -> {"Area" -> 0.001/2}];
mesh = ToElementMesh[reg];
groups = mesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1/(Length[groups])]];
colors = {ColorData["BrightBands"][#]} & /@ temp
mesh["Wireframe"["MeshElementStyle" -> FaceForm /@ colors]]

As you can see, the blue and yellow features represent the ends of the shape.

Now, you can refer to your DirichletCondition by ElementMarker like so:

{vals, funs} = 
  With[{em2 = (ElementMarker == 2), em3 = (ElementMarker == 3)}, 
   NDEigensystem[{stressOperator[10^3, 33/100], 
     DirichletCondition[u[x, y, z] == 0, em2], 
     DirichletCondition[v[x, y, z] == 0, em2], 
     DirichletCondition[w[x, y, z] == 0, em2], 
     DirichletCondition[u[x, y, z] == 0, em3], 
     DirichletCondition[v[x, y, z] == 0, em3], 
     DirichletCondition[w[x, y, z] == 0, em3]}, {u, v, 
     w}, {x, y, z} \[Element] mesh, 12]
   ];

When you plot the solution, you can see that both ends are fixed.

n = 6;
fac = 0.02;
uif = funs[[n, 1]];
vif = funs[[n, 2]];
wif = funs[[n, 3]];
dmesh = ElementMeshDeformation[mesh, {uif, vif, wif}, 
   "ScalingFactor" -> fac];
Show[mesh["Wireframe"], 
 dmesh["Wireframe"[
   "ElementMeshDirective" -> Directive[EdgeForm[Red], FaceForm[]]]], 
 Axes -> True, AxesLabel -> {"x", "y", "z"}]

Excellent solution. I will have to explore the markers more. Thanks. — Hugh, Jul 07 '21 at 13:44
Is BoundaryElementMarkerUnion Written up anywhere? I can find a little under ElemetMesh. I notice that as you change the area of the mesh elements the number of features you get changes. How does the code look for features? Is it to do with change in normal direction? Should I ask a new question on this? — Hugh, Jul 07 '21 at 14:30
@Hugh Thank you! They use it quite a bit in the OpenCascadeLink Tutorial. That is where I learned about it. — Tim Laska, Jul 07 '21 at 14:56
I can't resist writing that I find both the question and this answer quite impressive. I imagine they must have involved a lot of time and persistence. — Ralph Dratman, Jul 14 '21 at 04:53

user21 · Answer 2 · 2021-07-08T14:44:40.030

8

As Tim points out, using markers is the way to go. Here is another way to generate that torus:

Needs["OpenCascadeLink`"]
shape = OpenCascadeShape[
   OpenCascadeTorus[{{0, 0, 0}, {0, 0, 1}}, 1, 0.05, 0.654 \[Pi]]];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[shape, 
   "ShapeSurfaceMeshOptions" -> {(*"AngularDeflection"->0.5,*)
     "LinearDeflection" -> 0.001}];
bmesh["Wireframe"]

You can then visualize the mesh with its markers

groups = bmesh["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1/(Length[groups])]];
colors = ColorData["BrightBands"][#] & /@ temp;
Show[
 bmesh["Edgeframe"],
 bmesh["Wireframe"["MeshElement" -> "BoundaryElements", 
   "MeshElementStyle" -> (Directive[EdgeForm[], FaceForm[#]] & /@ 
      colors)]]
 , Epilog -> Inset[LineLegend[colors, groups], Scaled[{0.85, 0.8}]]
 ]

edited Jul 08 '21 at 14:44

answered Jul 07 '21 at 19:11

user21

39,710
8
110
167

Thanks useful as usual. There is a lot to learn here. Is the OpendCascade Tutorial the only place to learn from? – Hugh Jul 07 '21 at 21:31
@Hugh, yes, currently (V12.3) the tutorial is the only place. – user21 Jul 08 '21 at 04:54
2

(its = possessive, it's = "it is" or "it has". See for example https://www.youtube.com/watch?v=8Gv0H-vPoDc&t=1m20s and https://www.wikihow.com/Use-Its-and-It%27s) – Peter Mortensen Jul 08 '21 at 08:51
@PeterMortensen, fixed. thanks. – user21 Jul 08 '21 at 14:44

How can I make a region for boundary conditions for a 3D geometry?

2 Answers2