0

My problem is the yellow part is the partial derivative operator but i don't know how to put this expression because it has 2 problems The first problem it has 2 variables which are with respect to r and theta. The second problem i need to get the second derivative for an operator not just the first derivative for theta, I appreciate any help 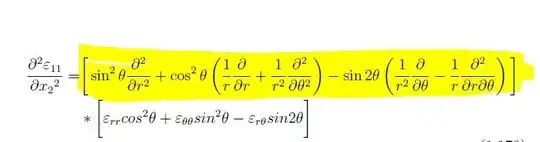enter image description here.

Magdy Ismail
  • 1
  • 1
  • Please check the document of D and Derivative. As to operators, we have many related posts e.g. https://mathematica.stackexchange.com/q/172482/1871 (Don't miss the links therein. ) – xzczd Jul 09 '21 at 07:51
  • Welcome to Mathematica.SE! I hope you will become a regular contributor. To get started, 1) take the introductory [tour] now, 2) when you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge, 3) remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign, and 4) give help too, by answering questions in your areas of expertise. – bbgodfrey Jul 09 '21 at 12:12

1 Answers1

2

Try Derivative !

Examplary D[eps[r, teta] Cos[teta]^2,{{r,teta}]

Derivative[1, 1][Function[{r, teta}, eps[r, teta] Cos[teta]^2] ][r, teta]
Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
  • Can i ask the use of [1,1] is for what? – Magdy Ismail Jul 09 '21 at 09:27
  • Means first derivative of the first/first derivative of the second variable. – Ulrich Neumann Jul 09 '21 at 10:07
  • Sorry for that but the whole answer is vague to me i mean i have the second partial derivative not just first derivative so can you write to me the whole equation in one line like that D[Function[{r, [Theta]}, Subscript[[Epsilon], rr] Cos[[Theta]]^2 + Subscript[[Epsilon], [Theta][Theta]] Sin[[Theta]]^2 - Subscript[[Epsilon], r[Theta]] Sin[[Theta]]^2]][r, [Theta]] – Magdy Ismail Jul 09 '21 at 11:28
  • My answer is examplary, but if you understand the syntax ( see documentation Derivative) you might apply it to all the other terms in your function. – Ulrich Neumann Jul 09 '21 at 11:45
  • I checked the syntax in ( documentation Derivative) and I wrote it like that but it seems not right Do you have any suggestion if the below code is right? – Magdy Ismail Jul 09 '21 at 14:04
  • oper = Function[{f, [Theta]}, (Sin[[Theta]]^2D[f[[Theta]], r ] D[f[[Theta]], r] + Cos[[Theta]] Cos[[Theta]]*D (1/r D[f[[Theta]], r] + 1/r^2) - Sin[2 [Theta]] (1/ r^2 D[f[[Theta]], [Theta]] D[f[[Theta]], [Theta]]))]; oper[fooo, [Theta]] fooo[[Theta]_] := Cos[[Theta]]^2 Subscript[[Epsilon], rr] + Sin[[Theta]]^2 Subscript[[Epsilon], [Theta][Theta]] - Sin[2 [Theta]] Subscript[[Epsilon], r[Theta]] oper[fooo, [Theta]] – Magdy Ismail Jul 09 '21 at 14:04