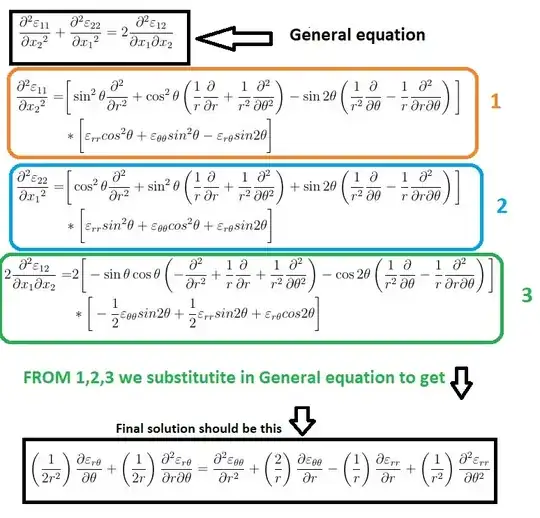
My main issue when I try to put all the equations in Mathematica ,I get different solution from what I expected should be,Epsilon 11,22,12 are functions and multiplied by Their partial derivative operator,Can anyone confirm if the written code is right?
Clear[op1, op2, op3]
Subscript[\[Epsilon], 11] = Subscript[\[Epsilon], rr]*Cos[\[Theta]]^2 + Subscript[\[Epsilon], \[Theta]\[Theta]]*Sin[\[Theta]]^2 -
Subscript[\[Epsilon], r\[Theta]]*Sin[2*\[Theta]] & ;
op1 = Sin[\[Theta]]^2*D[#1, {r, 2}] + Cos[\[Theta]]^2*(1/r)*D[#1, r] + Cos[\[Theta]]^2*(1/r^2)*D[#1, {\[Theta], 2}] -
Sin[2*\[Theta]]*(1/r^2)*D[#1, \[Theta]] + Sin[2*\[Theta]]*(1/r)*D[#1, r]*D[#1, \[Theta]] & ;
firstterm := TrigExpand[op1[Subscript[\[Epsilon], 11][f[r, \[Theta]]]] +
op1[f[r, \[Theta]]]*Subscript[\[Epsilon], 11][f[r, \[Theta]]]];
Subscript[\[Epsilon], 22] = Subscript[\[Epsilon], rr]*Sin[\[Theta]]^2 + Subscript[\[Epsilon], \[Theta]\[Theta]]*Cos[\[Theta]]^2 +
Subscript[\[Epsilon], r\[Theta]]*Sin[2*\[Theta]] & ;
op2 = Cos[\[Theta]]^2*D[#1, {r, 2}] + Sin[\[Theta]]^2*(1/r)*D[#1, r] + Sin[\[Theta]]^2*(1/r^2)*D[#1, {\[Theta], 2}] +
Sin[2*\[Theta]]*(1/r^2)*D[#1, \[Theta]] - Sin[2*\[Theta]]*(1/r)*D[#1, r]*D[#1, \[Theta]] & ;
secondterm := TrigExpand[op2[f[r, \[Theta]]]*Subscript[\[Epsilon], 22][f[r, \[Theta]]] +
op2[Subscript[\[Epsilon], 22][f[r, \[Theta]]]]];
SSSS = Expand[firstterm + secondterm];
Subscript[\[Epsilon], 12] = -0.5*Subscript[\[Epsilon], \[Theta]\[Theta]]*Sin[2*\[Theta]] + 0.5*Subscript[\[Epsilon], rr]*Sin[2*\[Theta]] +
Subscript[\[Epsilon], r\[Theta]]*Cos[2*\[Theta]] & ;
op3 = 2*(Sin[\[Theta]]*Cos[\[Theta]]*D[#1, {r, 2}] - Sin[\[Theta]]*Cos[\[Theta]]*(1/r)*D[#1, r] -
Sin[\[Theta]]*Cos[\[Theta]]*(1/r^2)*D[#1, {\[Theta], 2}] - Cos[2*\[Theta]]*(1/r^2)*D[#1, \[Theta]] +
Cos[2*\[Theta]]*(1/r)*D[#1, r]*D[#1, \[Theta]]) & ;
thirdterm = Expand[op3[f[r, \[Theta]]]*Subscript[\[Epsilon], 12][f[r, \[Theta]]] + op3[Subscript[\[Epsilon], 12][f[r, \[Theta]]]]];
TrigExpand[TrigExpand[thirdterm - SSSS]]
The solution that I get in Mathematica is like below
-((2*Subscript[\[Epsilon], r\[Theta]]*
Derivative[0, 1][f][r, \[Theta]])/r^2) -
(1.*Subscript[\[Epsilon], rr]*Derivative[0, 2][f][r, \[Theta]])/
r^2 -
(1.*Subscript[\[Epsilon], rr]*Derivative[1, 0][f][r, \[Theta]])/r +
(2*Subscript[\[Epsilon], r\[Theta]]*
Derivative[0, 1][f][r, \[Theta]]*
Derivative[1, 0][f][r, \[Theta]])/r -
1.*Subscript[\[Epsilon], \[Theta]\[Theta]]*
Derivative[2, 0][f][r, \[Theta]]
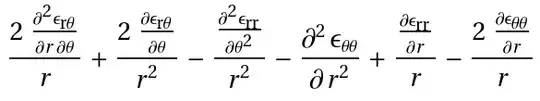
Subscript[ϵ, 11]. This is a function that does not use its arguments. – Daniel Huber Jul 18 '21 at 19:52Subscript[\[Epsilon], 11]to be an anonymous function of 2 variables (r and theta) you may e.g. write:Subscript[\[Epsilon], 11] = Subscript[\[Epsilon], rr][#1, #2]*Cos[\[Theta]]^2 + Subscript[\[Epsilon], \[Theta]\[Theta]][#1, #2]*Sin[\[Theta]]^2 - Subscript[\[Epsilon], r\[Theta]][#1, #2]*Sin[2*\[Theta]] &;– Daniel Huber Jul 19 '21 at 16:17