Speedup the production of a sparse symmetric matrix with a dense vector

Question

The optimization of the production of a sparse symmetric matrix with a dense vector has existed for a long time. Someone once compared the matrix operations of Mathematica with MATLAB, and then came to the conclusion: the slowness is due to the copying of the data. Now I want to solve this problem through Mathematica's LibraryLink, such as calling C++ Armadillo or C++ Eigen, without copying data. In the past, Szabolcs's LTemplate successfully called Armadillo, and Henrik Schumacher successfully called Eigen. Now I have three methods to calculate the production of a sparse symmetric matrix with a dense vector. I can use Mathematica alone, calling Armadillo through librarylink and calling Eigen through librarylink. My code as follow:

Construct a sparse symmetric matrix H

Clear["`*"]
n=300;
nn=n*n;
v=1.;
{minbegin,minend}={Range[n+1,(n-3)*n+1,2*n],Range[2*n,(n-2)*n,2*n]};
H0=SparseArray[Automatic,{nn,nn},0,{1,{Flatten[Range[0,nn-n,1]~Append~ConstantArray[nn-n,n]],n+{#}&/@Range[1,nn-n,1]},ConstantArray[v,nn-n]}]+SparseArray[(#->v)&/@({Table[{i,i+n-1},{i,Range[minbegin[[#]]+1,minend[[#]],1]}]&/@Range[Length[minbegin]]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+n*(n-1)},{i,1,n,1}]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+n*(n-1)+1},{i,1,n-1,1}]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+2*n-1},{i,minbegin}]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+n*(n-2)+1},{i,{n}}]}//Flatten//Partition[#,2]&),{nn,nn}];
H=H0+Transpose[H0];

Construct a dense vector

f1=(Cos[2*Pi*#]&/@RandomReal[{0,1},nn]);

only use Mathematica

 in:  AbsoluteTiming[H.H.H.H.H.H.H.H.H.H.f1 // Total]
out:  {1.6734,7.63163*10^6}

Write a function to call Armadillo to implement the production, where I use shared memory. (You need to install LTemplate and Armadillo)

Needs["LTemplate`"]
code="#include <LTemplate.h>
#define ARMA_COUT_STREAM mma::mout
#define ARMA_CERR_STREAM mma::mout
#include <armadillo>
template<typename T>
arma::Mat<T> toArmaTransposed(mma::MatrixRef<T> m) {
    return arma::Mat<T>(m.data(), m.cols(), m.rows(), false /* do not copy /, false / until resized */);
}
template<typename T>
mma::TensorRef<T> fromArmaTransposed(const arma::Mat<T> &m) {
    return mma::makeMatrix<T>(m.n_cols, m.n_rows, m.memptr());
}
template<typename T>
arma::Col<T> toArmaVec(mma::TensorRef<T> v) {
    return arma::Col<T>(v.data(), v.size(), false /* do not copy /, false / until resized */);
}
template<typename T>
mma::TensorRef<T> fromArmaVec(const arma::Col<T> &v) {
    return mma::makeVector<T>(v.size(), v.memptr());
}
template<typename T>
arma::SpMat<T> toArmaSparseTransposed(mma::SparseMatrixRef<T> sm) {
    return arma::SpMat<T>(
        arma::conv_to&lt;arma::uvec&gt;::from(toArmaVec(sm.columnIndices())) - 1, // convert to 0-based indices; Mathematica uses 1-based ones.
        arma::conv_to&lt;arma::uvec&gt;::from(toArmaVec(sm.rowPointers())),
        toArmaVec(sm.explicitValues()),
        sm.cols(), sm.rows()
       );

}
template<typename T>
mma::SparseMatrixRef<T> fromArmaSparse(const arma::SpMat<T> &am) {
auto pos  = mma::makeMatrix&lt;mint&gt;(am.n_nonzero, 2); // positions array
auto vals = mma::makeVector&lt;double&gt;(am.n_nonzero);  // values array

mint i = 0;
for (typename arma::SpMat&lt;T&gt;::const_iterator it = am.begin();
     it != am.end();
     ++it, ++i)
{
    vals[i] = *it;
    pos(i,0) = it.row() + 1; // convert 0-based index to 1-based
    pos(i,1) = it.col() + 1;
}

auto mm = mma::makeSparseMatrix(pos, vals, am.n_rows, am.n_cols);

pos.free();
vals.free();

return mm;

}
class Arma {
public:
mma::RealTensorRef ArmadilloDot(mma::SparseMatrixRef&lt;double&gt; mmaH, mma::RealTensorRef mmaf2) {

    arma::sp_mat H = toArmaSparseTransposed(mmaH);
    arma::vec f2 = toArmaVec(mmaf2);
    arma::vec F3;

    F3 = H*H*H*H*H*H*H*H*H*H*f2;

    return fromArmaVec&lt;double&gt;(F3);
}



};";
Export["Arma.h",code,"String"]
template=
LClass["Arma",
{
LFun["ArmadilloDot",{{LType[SparseArray,Real,2],"Shared"},{Real,1,"Shared"}},{Real,1}]
}
];
CompileTemplate[template,
"IncludeDirectories"->{"C:\Users\sidy\AppData\Roaming\Mathematica\Applications\LTemplate\armadillo-10.5.1\include"},
"LibraryDirectories"->{"C:\Users\sidy\AppData\Roaming\Mathematica\Applications\LTemplate\armadillo-10.5.1\examples\lib_win64"},
"Libraries"->{"libopenblas"},"CompileOptions"->{"-std=c++11","-O2","-fopenmp"}]
LoadTemplate[template]
arma=Make[Arma]

 in:  AbsoluteTiming[arma@"ArmadilloDot"[H, f1] // Total]
out:  {1.11007,7.63163*10^6}

Write a function to call Eigen to implement the production, where I use shared memory. (You need to install Eigen)

srcpath="~";
outpath="~";
Needs["CCompilerDriver`"];
Module[{opts,path,file,lib},If[!FileExistsQ[srcpath],CreateDirectory[srcpath]];
If[!FileExistsQ[outpath],CreateDirectory[outpath]];
file=Export[FileNameJoin[{srcpath,"cClipGeneralizedEigenvalues.cpp"}],"
#include <iostream>
#include <vector>
#include&quot;WolframLibrary.h&quot;
#include &quot;WolframSparseLibrary.h&quot;
#include<Eigen/Eigenvalues>
#include <Eigen/Sparse>
using namespace std;
using namespace Eigen;
EXTERN_C DLLEXPORT int cClipGeneralizedEigenvalues(WolframLibraryData libData, mint Argc, MArgument *Args, MArgument Res)
{
    MTensor MArow = MArgument_getMTensor(Args[0]);
    MTensor MAcol = MArgument_getMTensor(Args[1]);
    MTensor MAval = MArgument_getMTensor(Args[2]);
    MTensor MBvec = MArgument_getMTensor(Args[3]);
    MTensor MCout;
    libData->MTensor_new(MType_Real, 1, libData->MTensor_getDimensions(MBvec), &MCout);
    mint Mlength = MArgument_getInteger(Args[4]);
    mint n = MArgument_getInteger(Args[5]);
Eigen::Map<Eigen::VectorXd >Arow(libData->MTensor_getRealData(MArow),Mlength);
Eigen::Map<Eigen::VectorXd >Acol(libData->MTensor_getRealData(MAcol),Mlength);
Eigen::Map<Eigen::VectorXd >Aval(libData->MTensor_getRealData(MAval),Mlength);
Eigen::Map<Eigen::VectorXd >B(libData->MTensor_getRealData(MBvec),n);
Eigen::Map<Eigen::VectorXd >C(libData->MTensor_getRealData(MCout),n);
Eigen::SparseMatrix<double> A(n, n);
vector < Triplet < double > > triplets ;
for ( int i = 0 ; i < Mlength ; ++ i )
    {
        triplets . emplace_back ( Arow(i) , Acol(i) , Aval(i)) ; 
    }
A . setFromTriplets ( triplets . begin ( ) , triplets . end ( ) ) ;
C = AAAAAAAAAAB;
MArgument_setMTensor(Res, MCout);
return 0;
}","Text"];
lib=CreateLibrary[{file},"cClipGeneralizedEigenvalues","TargetDirectory"->outpath,"IncludeDirectories"->{"C:\Users\sidy\AppData\Roaming\Mathematica\Applications\eigen-3.4-rc1"},"CompileOptions"->{"-std=c++11","-O2","-fopenmp"}];
With[{libfile=lib},cClipGeneralizedEigenvalues::usage="";
cClipGeneralizedEigenvalues:=cClipGeneralizedEigenvalues=LibraryFunctionLoad[libfile,"cClipGeneralizedEigenvalues",{{Real,1,"Shared"},{Real,1,"Shared"},{Real,1,"Shared"},{Real,1,"Shared"},Integer,Integer},{Real,1,Automatic}];]]

 in:  HCSR=ArrayRules[H][[1;;-2]]/.Rule->List//Flatten//Partition[#,3]&;
      {row,col,val}={HCSR[[;;,1]]-1,HCSR[[;;,2]]-1,Developer`ToPackedArray[HCSR[[;;,3]]]};
      AbsoluteTiming[cClipGeneralizedEigenvalues[row,col,val,f1,Length[val],nn]//Total]
out:  {2.0971,7.63163*10^6}

Compare

tab=Table[
nn=n*n;
v=1.;
{minbegin,minend}={Range[n+1,(n-3)*n+1,2*n],Range[2*n,(n-2)*n,2*n]};
H0=SparseArray[Automatic,{nn,nn},0,{1,{Flatten[Range[0,nn-n,1]~Append~ConstantArray[nn-n,n]],n+{#}&/@Range[1,nn-n,1]},ConstantArray[v,nn-n]}]+SparseArray[(#->v)&/@({Table[{i,i+n-1},{i,Range[minbegin[[#]]+1,minend[[#]],1]}]&/@Range[Length[minbegin]]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+n*(n-1)},{i,1,n,1}]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+n*(n-1)+1},{i,1,n-1,1}]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+2*n-1},{i,minbegin}]}//Flatten//Partition[#,2]&),{nn,nn}]+SparseArray[(#->v)&/@({Table[{i,i+n*(n-2)+1},{i,{n}}]}//Flatten//Partition[#,2]&),{nn,nn}];
H=H0+Transpose[H0];
f1=(Cos[2*Pi*#]&/@RandomReal[{0,1},nn]);
{AbsoluteTiming[arma@"ArmadilloDot"[H,f1]//Total][[1]],
AbsoluteTiming[H.H.H.H.H.H.H.H.H.H.f1//Total][[1]],
HCSR=ArrayRules[H][[1;;-2]]/.Rule->List//Flatten//Partition[#,3]&;
{row,col,val}={HCSR[[;;,1]]-1,HCSR[[;;,2]]-1,Developer`ToPackedArray[HCSR[[;;,3]]]};
AbsoluteTiming[cClipGeneralizedEigenvalues[row,col,val,f1,Length[val],nn]//Total][[1]]},{n,100,1000,100}]
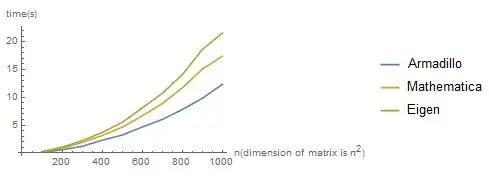
ListLinePlot[{Thread[{Range[100,1000,100],tab[[;;,1]]}],Thread[{Range[100,1000,100],tab[[;;,2]]}],Thread[{Range[100,1000,100],tab[[;;,3]]}]},PlotLegends->{"Armadillo","Mathematica","Eigen"},AxesLabel->{"n(dimension of matrix is n^2)","time(s)"}]

I found that Armadillo took the shortest time, followed by Mathematica and finally by Eigen. Is there any way to speed up my code?

Better use Dot[matrix, Dot[matrix, vectror]] to ensure matrix vector priduct, try low level functions, e.g. https://reference.wolfram.com/language/LowLevelLinearAlgebra/ref/SYMV.html, or call blas directly, another option is to use cuda variant of blas — I.M., Jul 22 '21 at 17:33

score 6 · Answer 1 · answered Jul 22 '21 at 17:33

6

You don't need a library. This is already optimized in Mathematica. On my machine

RepeatedTiming[t1 = H.H.H.H.H.H.H.H.H.H.f1;]
RepeatedTiming[t2 = MatrixPower[H, 10, f1];]

take 1.00s and 0.0032s respectively, for $>$ 300x speed-up.

Note also that the slow part of your code is not the multiplication of a matrix and a vector, it's the multiplication of the matrices themselves. On my machine

RepeatedTiming[t1 = H.H.H.H.H.H.H.H.H.H;]
RepeatedTiming[t2 = H.H.H.H.H.H.H.H.H.H.f1;]

Take 0.98s and 1.00s respectively with RepeatedTiming[t3 = t1.f1;] taking only 0.0052s

This is likely why using MatrixPower, especially the version times a vector, is so efficient.

answered Jul 22 '21 at 17:33

MathematicaLover

61
3

2

Very good idea to use MatrixPower! (+1) Already Nest[H . # &, f1, 10] would haven given a major performance boost, showing that this is not black magic. – Henrik Schumacher Jul 22 '21 at 20:27
@HenrikSchumacher I'd assert the fact that the Nest imp is so much faster than the naive one does indicate some level of black magic (unless I am missing something in expecting that speedup to be related to like autocomp. or something) – b3m2a1 Jul 23 '21 at 00:09
@HenrikSchumacher I see a little black magic. If I Quit then run the init code and RepeatedTiming[Total[MatrixPower[H, 10, f1]]], RepeatedTiming[Total[Nest[H . # &, f1, 10]]] and RepeatedTiming[ Total[H .(H.(H.(H.(H.(H.(H.(H.(H.(H.f1)))))))))]] I'll get times differing by up to a factor of 6, depending on which order I do them. On the other hand, if I run a filler line like Table[x, {x, 20}] I get more like a factor of 2. If I run ParallelTable[x, {x, 20}] or just rerun everything again there's no difference. Mathematica is initializing something non-trivial under the hood. – MathematicaLover Jul 23 '21 at 00:30
1

@MathematicaLover Ah, I see. I can confirm this behavior (version 12.3.1 for macos), but only if I place everything into a single cell. Even more mysterious: The timings are always something like 0.00229355, 0.00870448, 0.0055025---in that order, no matter what the order of the three lines is. Indeed, Mathematica has often a one-time cost when you run a function for the first time in a session because many packages are loaded lazily. And also the MKL may have some one-time costs (allocation of some buffers). But this does not explain these weird timings... – Henrik Schumacher Jul 23 '21 at 04:34

Henrik Schumacher · Answer 2 · 2021-07-22T21:06:52.123

Not an answer, but some extended comments.

Sparse matrix-sparse matrix multiplication

MathematicaLover made the very good observation that--as written by OP--Mathematica performs sparse matrix-sparse matrix multiplies. In fact, Armadillo does it, too, it seems to be about twice as fast in that. I was quite surprised by the great margin by which Armadillo was so much faster. Now I believe that I have an explanation for that: The compiler is probably clever enough to optimize in the following spirit:

First@AbsoluteTiming[
  H10slow = H.H.H.H.H.H.H.H.H.H;
  Total[H10slow.f1];
  ]
First@AbsoluteTiming[
  H2 = H.H;
  H4 = H2.H2;
  H10 = H2.H4.H4;
  Total[H10.f1];
  ]
H10 == H10slow

1.27093

0.440999

True

Compared to this, the Armadillo function takes 0.631295 on my machine (which is an Intel Haswell, so an architecture for which the MKL is highly optimized).

Hence Armadillo does not seem to be really better than Mathematica+MKL in this benchmark; it is the C++ compiler that made the difference (because it is able to do what I did by hand).

Sparse matrix-vector multiplication

So, let's also compare Armadillo's sparse matrix-vector multiplication to Mathematica's (or rather that of MKL). To that end I compiled the function ArmilloDot with

F3 = H*H*H*H*H*H*H*H*H*H*f2;

replaced by

F3 = H*(H*(H*(H*(H*(H*(H*(H*(H*(H*f2)))))))));

Then I ran

RepeatedTiming[Total[arma@"ArmadilloDot"[H, f1]]]
RepeatedTiming[Total[Nest[H.# &, f1, 10]]]
RepeatedTiming[Total[MatrixPower[H, 10, f1]]]

and got these as results:

{0.0148027, -9.3592*10^6}

{0.00386909, -9.3592*10^6}

{0.00334479, -9.3592*10^6}

So the Armadillo variant is actually awfully slow!

Disclaimer

Once again, all timing results are strongly hardware and software dependent. I only tried to point out that performance tests have to be made thoroughly. And that MKL is a really good math library --- if you use an Intel CPU. It is however notorious for nerfing AMD CPUs.

Speedup the production of a sparse symmetric matrix with a dense vector

2 Answers2

Sparse matrix-sparse matrix multiplication

Sparse matrix-vector multiplication

Disclaimer