0

My code produces the iconic figure showing the error threshold of the quasispecies model.

Clear["Global`*"]
L = 10
n = L+1

f = ConstantArray[1, n]
f[[1]] *= 10
f


tMax = 10^4


MatrixForm[
q =
Table[
    Sum[
           u ^   (i+j-2k) 
        (1-u)^(L-(i+j-2k))
        Binomial[L-i,j-k]*
        Binomial[  i,  k],
        {k,Max[0,i+j-L],Min[i,j]}],
    {i,0,L},{j,0,L}]
]


DiffEqn =
Table[
      Dt[x[i][t], t] == Sum[x[j][t]f[[j]]q[[j,i]], {j,n}] - Sum[x[i][t]f[[i]], {i,n}]x[i][t],
      {i,n}
      ]


solution =
ParametricNDSolve[
    {DiffEqn, Table[x[i][0] == 1/n, {i,n}]},
    Table[x[i], {i,n}],
    {t,0,tMax},
    {u}]


figure =
Plot[Evaluate[Table[x[i][u][tMax], {i,n}]/.solution],
     {u,0,1},
     PlotRange->{{0,1},{0,1}},
     PlotLegends->Placed[Range[n]-1,Below]]

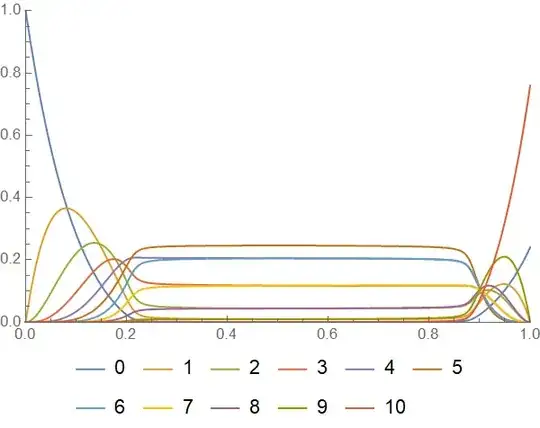
Beautiful.

Now, I would like to add another dimension to the figure by plotting the curves of the different error classes separately along an additional axis.
There are several questions and answers on this site about this, e.g. this Q&A and the questions linked therein. So my question might well be a duplicate.
But I've tried and failed miserably to produce the desired figure based on the other Q&As.

figure2 =
ParametricPlot3D[Evaluate[Table[i-1,u,x[i][u][tMax], {i,n}]/.solution],
                 {u,0,1}]

I don't know where I was mistaken. But I'm not sure I understand how I should use the ParametricFunction objects (produced by ParametricNDSolve) with ParametricPlot3D.

rokamama
  • 103
  • 5
  • Please include in your question the code that "failed miserably".. – bbgodfrey Jul 28 '21 at 14:29
  • @bbgodfrey I edited the question with my code that was closest to the solution. Unfortunately, after that, I went in a completely wrong direction. I'm terribly sorry. The Q&A you linked is exactly the same as I linked. In hindsight, it answers my question. I don't know how I could not adapt it to my problem. Embarrassing... – rokamama Jul 28 '21 at 15:16

1 Answers1

2

Use ParametricPlot3D. You can change the distance between curves with dist.

dist = 1/10;
ParametricPlot3D[
 Evaluate[
  Table[{u, dist*i, x[i][u][tMax]}, {i, n}] /. solution
  ], {u, 0, 1}]

Mathematica graphics

Domen
  • 23,608
  • 1
  • 27
  • 45